lozty писал(а):
Привет!
Может кто знает? стандартные функции, на которых проверяются методы оптимизации первого порядка? (в частности кубической аппроксимации)
Заранее спасибо.
Обычно алгоритмы оптимизации теститруются на функциях с хорошими "оврагами" - длинными, глубокими, извилистыми. Простейший пример (для 2-х переменных) - функция Розенброка:

, где
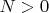
- достаточно большое число (обычно 100).
Вспоминаются еще функции Пауэлла, Вуда. Но не помню точного вида, а в Сети с ходу не нашел.
Нашел зато еще несколько функций для тестирования алгоритмов оптимизации:
http://www.orc.ru/~pulsar/test/test_r.htmlНадеюсь, этого вам хватит?



