Предлагаю рассмотреть и обсудить интерпретацию квантовой механики, которая, на мой взгляд, может следовать из общей теории относительности. При этом, естественно, в теорию следует ввести дополнительно новую константу — постоянную Планка, и принять некоторую рабочую гипотезу.
Я сформулирую рабочую гипотезу следующим образом:
Искривление пространства порождает энергию, которая в свою очередь усиливает искривление этого пространства.Пусть мы имеем дело с гравитирующим телом, которое издали можно считать сферически симметричным. Тогда элемент пространственной радиальной длины вдали от него можно определить формулой:

Здесь

– потенциал гравитационного поля. Он и определяет искривление пространства.
Согласно высказанной гипотезе в формуле следует произвести замену:

В свою очередь добавку
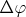
можно представить в виде:

Параметр

представляет собой добавку, связанную параметром самой задачи – ее характерным гравитационным радиусом :

здесь
a — универсальная константа, равная корню из произведения гравитационного и комптоновского радиуса частиц, так что:

Гравитационный радиус связан с потенциалом:

Введем в наши формулы искусственно постоянную Планка и запишем добавку к потенциалу в виде:

Введем новую величину

которая имеет векторный характер, имеет размерность импульса, но не определяет и не характеризует никакого движения. Назовем ее статическим геометрическим импульсом. Привлекая формулу для
a, окончательно имеем:

С учетом такой поправки, например, в метрике Шварцшильда нужно будет произвести замену

Объект ведет себя так, как если бы его масса стала функцией
r. Если в качестве массы выбрать массу электрона, то такая зависимость для
r>
a определилась бы формулой:

Объект теперь локализуется не своим гравитационным радиусом, а «размазывается» далеко за его пределы. Теперь для описания его поведения нужен несколько иной подход. На помощь приходит квантовая механика.
Рассмотрим функцию Лагранжа для обычной скалярной частицы:

Комплексно-значная волновая функция может быть представлена в виде:

С учетом этого лагранжиан может быть переписан в виде:

где

уже определенный выше статический геометрический импульс, а

обычный динамический импульс. Заметим, что геометрический импульс является пространственно-подобным, а динамический – времени-подобным. Принцип наименьшего действия для лагранжиана, получается, состоит в том, что усредненные суммы квадратов всех видов импульсов частицы максимально близки к квадрату собственного импульса частицы
mc.
Плотность в интеграле действия вполне может восприниматься в своей обычной квантово-механической интерпретации – плотности вероятности пребывания частицы в некоторой области пространства. Аналогично, можно интерпретировать эту величину как плотность представления частицы в той же области, т.е. плотности того, как представлена частица в той или иной области своими динамическими или статическими геометрическими импульсами.