Hi again. Here is what I have done.
Because
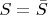
than

is complete subspace of
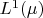
.
Let
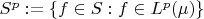
for

From
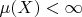
we have that -
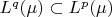
for some
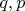
set to
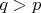
and
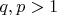
. That implicates
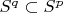
for
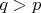
.
Now we can make sequence
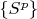
just to use that indexes

which are in
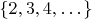
and in
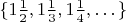
(we don't need all
![$(1,\infty]$). $(1,\infty]$).](https://dxdy-03.korotkov.co.uk/f/6/f/2/6f297dc344e4659b92d20392137d67b082.png)
So let that be index set
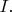
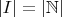
.
We now have that
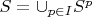
. From this we can even form a disjoint family of subsets
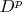
so that
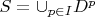
.
By the one version of Baire Category Theorem, there exists
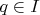
so that closure
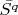
has an interior point (we can say that for
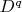
respectively). Let that interior point (function) be
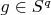
. That means that it has a ball around itself for some
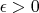
-
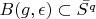
and of course
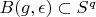
too.
Now all elements in

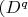
if we are looking on it simultaneously) can be written like linear combination of some element from
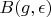
.
But now what?
We can assume opposite that exists
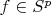
where
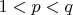
and
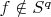
(same thing can be said for
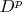
and
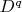
). But again, I don't see anything useful with I can do something... So, please help.
I don't speak Russian very well, but understand it (freely write suggestions on Russian).
Спасибо.



