Можно ли это описать с помощью тета-функции Хевисайда следующим образом:
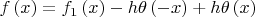
?
Как-то сомнительно, возьмите например:
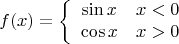
А производная от нее:
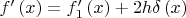
?
А вот это верно. Ну разве что для поборников строгости надо дописать, что исходная

гладкая и

почти всюду равна

Раз функция
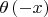
убывает, значит производная от нее должна быть отрицательной. Верно ли это утверждение в применении к обобщенным функциям?
А что такое "отрицательная обобщенная функция" в общем случае. Например функция

она отрицательная? Да и тета-функция она не совсем "убывает", она, если хотите, скорее "не возрастает"