Сопряженные к взвешенным L_{\infty}

[id]

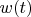
Интересует описание сопряженного пространства к взвешенному варианту $L_{\infty}$, где норма задается как $\sup\limits_{t \in X} \frac {f(t)} {w(t)}$, $X$ - можно считать, что это либо отрезок, либо $[0,+\infty)$, $w(t)$ - вес ( особенно интересует случай вогнутой/квазивогнутой функции ). ( У Шварца есть разобранный общий случай для $L^*_{\infty}$, но про вес ничего не сказано, а хотелось бы быть уверенным )

Так же интересует слабая компактность в данном пространстве ( но тут даже у Шварца для невзвешенного случая никакого удовлетворительного ответа нет, ограничивается отсылкой к определенному изометрическому изоморфизму с пространством непрерывных функций ).

Если есть литература/статьи, в которых подобные вопросы рассматриваются, интересно было бы ознакомиться.

[id]

Вопрос, похоже, не вызвал интереса. Так или иначе, ответ мне неизвестен и интересен.

Тогда еще один.
А какое будет сопряженное к пространству функций ограниченной вариации? ( в общем случае. Ну или хотя бы для $V[a,b]$ )

[AD]

id в сообщении #233456 писал(а):

А какое будет сопряженное к пространству функций ограниченной вариации?

Я тоже этот вопрос тут задавал, говорят, никто не знает. Сейчас поищу.

-- Пт авг 07, 2009 14:15:56 --

Вот: post121675.html#p121675

[id]

Эх, жаль.

Спасибо, AD!

P.S. Первый вопрос про сопряженные к взвешенным так или иначе еще открыт.

[Юстас]

Посмотрите на всякий случай в Богачёве, "Теория меры".

[id]

Юстас
Спасибо, посмотрел, но там вроде точно такого нет.

Хотя по поводу оригинального вопроса у меня уже есть версия, а именно что тут сопряженное изоморфно ( или даже изометрично ) $V[a,b]$ или $V[0,+\infty)$, только функционал задается по-другому ( чем для обычного $L^{\infty}$ ):
$g(f) = \int \frac {f(t)} {w(t)} dg(t)$. Ограниченность - из теоремы о среднем ( как для функционала на $L^{\infty}$).
Обратно, пусть $g(f)$ - функционал на нашем $E$. Тогда $g(f) = g ( w \frac f w ) = g(w h)$, где $g(w h)$ - функционал на $h(t) \in L^{\infty}$.

-- Ср авг 12, 2009 18:22:06 --

Меня вообще интересует второе сопряженное к таким пространствам. Если предположение выше верно, получается, что оно не зависит от весовой функции и равно V[0,+\infty)*, для которого никакого разумного описания нет?