Так о чем арифметика?

[Yarkin]

Sergey-Cop в сообщении #230156 писал(а):

Что значит, зарубки абстрактны? — это также перечисляемые объекты, как и камушки. Отличаются лишь тем, что зарубки — это запись на чём-то (на палочке, на дощечке). Это типа рисунок, знак, письменность. Непонятно, что подразумевается под "абстрактные": Письменный символ имеет абстрактный образ — наверное, это.

Камешек и зарубка (черточка) - это две различные ступени изображения пересчитываемого объекта. Переход от материальной модели к изображаемой влечет появление абстракции.

[Sergey-Cop]

Yarkin в сообщении #230694 писал(а):

Sergey-Cop в сообщении #230156 писал(а):

Что значит, зарубки абстрактны? — это также перечисляемые объекты, как и камушки. Отличаются лишь тем, что зарубки — это запись на чём-то (на палочке, на дощечке). Это типа рисунок, знак, письменность. Непонятно, что подразумевается под "абстрактные": Письменный символ имеет абстрактный образ — наверное, это.

Камешек и зарубка (черточка) - это две различные ступени изображения пересчитываемого объекта. Переход от материальной модели к изображаемой влечет появление абстракции.

Ну, только осталось понять, что подразумевается под словом «абстракция».

Берем толковый словарь (Ушакова):
1) Мысленное отделение каких-нибудь свойств и признаков предмета от самого предмета
2) Неясное, туманное выражение мысли

Ну вот, берем камушки, но подразумеваем отнюдь не камушки, а их количественное свойство. Хоть камушки, хоть палочки — всё равно. Смотрим только на количество, мысленно отделяя его «от самого предмета».

[Yarkin]

Sergey-Cop в сообщении #230804 писал(а):

Ну вот, берем камушки, но подразумеваем отнюдь не камушки, а их количественное свойство. Хоть камушки, хоть палочки — всё равно. Смотрим только на количество, мысленно отделяя его «от самого предмета».

Камушками мы заменили пересчитываемые объекты. Количество камушков равно количеству этих объектов, если под одним камушком подразумевается один объект. Что Вы имеете в виду под "количественным свойством"?

[Barsal]

Что такое арифметика я объяснял молодым школьникам таким образом:
(правда таблица была подлиннее)

111111111111111111111111111111111111111111111
101010101010101010101010101010101010101010101
100100100100100100100100100100100100100100100
100010001000100010001000100010001000100010001
100001000010000100001000010000100001000010000
100000100000100000100000100000100000100000100
100000010000001000000100000010000001000000100
100000001000000010000000100000001000000010000
и т.д.
хорошо видны делители чисел (вертикальные единицы), распределение простых чисел (вертикальные нули) и т.д

[Свободный Художник]

epros в сообщении #229448 писал(а):

Свободный Художник в сообщении #229440 писал(а):

epros в сообщении #229417 писал(а):

Кстати, касательно "чёрточек": Тут в параллельной ветке, обсуждая возможности дать определение тому, что понятие "определено в теории", мы предварительно пришли к выводу, что в теориях, содержащих константы, могут быть определены операции и отношения на вполне конкретных объектах, представляющих собой замкнутые термы теории. Например, для арифметики Пеано таковыми объектами являются строки $0$, $S(0)$, $S(S(0))$, ...

Ну, так это вроде как бы классика:
Агафонов В. Н., Борщев В. Б., Воронков А. А.
Логическое программирование в узком смысле.
В книге: Логическое программирование: Сборник статей. Под ред. Агафонова В. Н.
М.: Мир, 1988, сс. 302 — 303.
http://www.px-pict.com/9/6/4/4/1.html

Ну так а что Вы тогда спрашиваете "что изучает арифметика" да "в чём природа чисел"? Вот Вам "сами числа" - те самые, которые определены арифметикой: $0$, $S(0)$, $S(S(0))$, ...

Свободный Художник в сообщении #229608 писал(а):

Конечно, в определенном смысле синтаксические объекты $0, S(0), S(S(0)), $… более других способны претендовать на роль “платиново-иридиевый эталонов” для натуральных чисел.

Если выразиться по научному, то синтаксические “платиново-иридиевые эталоны” $0, S(0), S(S(0)), …$ для натуральных чисел образуют “универсум Эрбрана”:
Нильсон Н. Искусственный интеллект.
М.: Мир, 1973, сc. 172 — 204.
http://www.px-pict.com/9/6/2/4/2/1/6.html

Термы $0, S(0), S(S(0)), …$ образуют универсум Эрбрана для некоторой теории первого порядка, содержащей в своей сигнатуре единственную индивидную константу $0$ и единственный унарный функциональный символ $S$ (о предикатных символах этой теории пока помолчим).

[Barsal]

Прощайте математики, Вы бродите от одной ясности к другой.
Вас всех объединяет одно - потеря творчества, и Вы это знаете, лучше меня.

[AGu]

Barsal в сообщении #231025 писал(а):

Прощайте математики, Вы бродите от одной ясности к другой.
Вас всех объединяет одно - потеря творчества, и Вы это знаете, лучше меня.

Ну что ж, прощайте, Barsal. Вы бродите от одной туманности к другой. Вас отличает многое, включая потерю четкости определений и ясности изложения. И Вы этого, похоже, не знаете.

P.S. Простите, не смог удержаться от сарказма.

[Sergey-Cop]

Yarkin в сообщении #230857 писал(а):

Sergey-Cop в сообщении #230804 писал(а):

Ну вот, берем камушки, но подразумеваем отнюдь не камушки, а их количественное свойство. Хоть камушки, хоть палочки — всё равно. Смотрим только на количество, мысленно отделяя его «от самого предмета».

Камушками мы заменили пересчитываемые объекты. Количество камушков равно количеству этих объектов, если под одним камушком подразумевается один объект. Что Вы имеете в виду под "количественным свойством"?

Вообще-то вопрос стоял об абстракциях.
В соответствии с определением, данном в толковом словаре, камушки для счета — это абстракция. Это понятно или нет? — сначала надо закончить с одним вопросом.
Для счета нас интересуют не камушки как таковые, а их количество — это и есть абстракция (по определению).

Во-вторых. Исходная тема:

Свободный Художник в сообщении #225556 писал(а):

Что изучается в арифметике: числа или операции над ними?

Т.е. это вопрос не о том, что кто-либо имеет в виду под "количественным свойством", а что «имеет в виду» арифметика. Изучает ли она природу чисел или каждый уже заранее должен знать, что это за «количественное свойство».

[Профессор Снэйп]

Свободный Художник в сообщении #225556 писал(а):

Что изучается в арифметике: числа или операции над ними?..

Арифметика --- это наука о свойствах модели $\langle \mathbb{N}; +, \cdot, \leqslant, 0, 1 \rangle$. Естественно, модель достаточно задать с точностью до изоморфизма. В этом смысле природа самих по себе чисел действительно не важна

-- Пн июл 27, 2009 15:58:19 --

То же самое с матаном. Сия наука изучает свойства полного упорядоченного архимедова поля. Как конкретно задавать элементы этого поля --- вопрос второстепенный.

[Свободный Художник]

Свободный Художник в сообщении #230199 писал(а):

А как насчет арифметики Пресбургера? Тоже, ведь, арифметика как-бы …
http://en.wikipedia.org/wiki/Presburger_arithmetic
http://mathworld.wolfram.com/PresburgerArithmetic.html

Строим модель для арифметики Пресбургера следующим образом.
В качестве элементов множества-носителя модели берем аликвотные дроби (т. е. дроби вида $1/n$, где $n$ – некоторое натуральное число).
В качестве операции сложения берем операцию $\circ$:

Свободный Художник в сообщении #144753 писал(а):

Например, если определить систему: $\mathbf{Q^+} =\: <\! \mathrm{Q^+}, \bullet\,, \circ\,, \overline{\phantom{a}} >$,
где $\mathrm{Q^+}$ есть множество положительных рациональных чисел;
$\bullet$ есть бинарная операция на множестве $\mathrm{Q^+}$, определяемая как $x \bullet y = x + y$;
$\circ$ есть бинарная операция на множестве $\mathrm{Q^+}$, определяемая как $x \circ y = \dfrac{xy}{x + y}$;
$\overline{\phantom{a}}$ есть унарная операция на множестве $\mathrm{Q^+}$, определяемая как $\overline{x} = \dfrac1{x}$;
то в системе $\mathbf{Q^+}$ будут справедливы многие законы, имеющие место быть в булевой алгебре, например, законы де Моргана: $\overline{x \bullet y} = \overline{x} \circ \overline{y}$ и $\overline{x \circ y} = \overline{x} \bullet \overline{y}$.

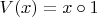
Операция $V(x) = x \circ 1$ “пашет” на аликвотных дробях точно так же, как и обычная операция $S(x) = x + 1$ “следующий за” на натуральных числах.
В качестве нуля берем бесконечность:

Свободный Художник в сообщении #172676 писал(а):

А вот элементы $0$ и $\infty$ -– не определимы в $\mathbf{Q^+}$, поэтому, если мы хотим говорить о них, то должны явно добавить их в сигнатуру системы, что, пользуясь случаем, я и делаю:

$\mathbf{Q^+_{\, 0,\: \infty}} =\: <\! \mathrm{Q^+}, \bullet\,, \circ\,, \overline{\phantom{a}}\,, 0\,, \infty >$

И, естественно, добавить еще аксиомы вида:
$x \bullet 0 = x\,, \; x \circ \infty = x \,;$
$x \bullet \infty = \infty\,, \; x \circ 0 = 0 \,;$
$\overline{0} = \infty\,, \; \overline{\infty} = 0\,;$
Здесь мы действительно добавили “новое” в $\mathbf{Q^+}$, поэтому и $\mathbf{Q^+_{\, 0,\: \infty}}$ -- новая система по отношению к $\mathbf{Q^+}$.

В результате получаем изоморфную реализацию для “стандартной” модели арифметики Пресбургера.
Это как-то разрушает стереотип, что арифметика Пресбургера (или даже арифметика Пеано) – наука о целых числах.
С равным успехом она может рассматриваться и как наука о дробных числах.

[Yarkin]

Профессор Снэйп в сообщении #231342 писал(а):

Арифметика --- это наука о свойствах модели

Интересно, что Вы подразумеваете под моделью?

-- Пт июл 31, 2009 22:47:07 --

Sergey-Cop в сообщении #231063 писал(а):

Для счета нас интересуют не камушки как таковые, а их количество — это и есть абстракция (по определению).

По какому определению? Количество это реально существующее число камешков - моделей подразумеваемых объектов - никакой абстракции нет.

[STilda]

Камешки моделируют коров, в этом и есть абстракция. Переход совершился от счета натуральных коров к счету объектов их обозначающих. Тоесть избавились от необходимости в коровах. Математика сей час ой как оторвана от реальности, сама в себе, можно сказать, варится. Вот это и есть абстракция.
Про понятие "Количество" никто тогда не говорил.

[naiv1]

STilda в сообщении #232552 писал(а):

Камешки моделируют коров, в этом и есть абстракция. Переход совершился от счета натуральных коров к счету объектов их обозначающих. Тоесть избавились от необходимости в коровах.

Вот мне нужно замостить двор плитками-камешками. Чем я буду моделировать камешки? Неужто мне придется наоборот коровами их моделировать? Да у меня никаких денег не хватит на такие модели! Какая уж тут абстракция. Это вполне живая конкретика. Тут что-то не то.

[Sergey-Cop]

Yarkin в сообщении #232325 писал(а):

Sergey-Cop в сообщении #231063 писал(а):

Для счета нас интересуют не камушки как таковые, а их количество — это и есть абстракция (по определению).

По какому определению? Количество это реально существующее число камешков - моделей подразумеваемых объектов - никакой абстракции нет.

Ха . Минут 15 ржал. Сейчас пойдем по кругу, возвращаясь к ранее данному определению, вновь проходя все аргументы. А потом опять и опять по кругу.

Sergey-Cop в сообщении #230804 писал(а):

Yarkin в сообщении #230694 писал(а):

Sergey-Cop в сообщении #230156 писал(а):

Что значит, зарубки абстрактны? — это также перечисляемые объекты, как и камушки…

Камешек и зарубка (черточка) - это две различные ступени…

…
Берем толковый словарь (Ушакова):
1) Мысленное отделение каких-нибудь свойств и признаков предмета от самого предмета
2) Неясное, туманное выражение мысли

Ну вот, берем камушки, но подразумеваем отнюдь не камушки, а…

Определений два. По первому; по первому определению.


Yarkin и naiv1, то что вы называете «абстракцией» в русском языке принято называть словом «вымысел». Вот так.

Вот то, что уж совсем оторвано от реальности — это вымысел.
(«Вымысел» по словарю Ушакова: «что-нибудь созданное воображением»)

[Свободный Художник]

Профессор Снэйп в сообщении #231342 писал(а):

Арифметика --- это наука о свойствах модели $\langle \mathbb{N}; +, \cdot, \leqslant, 0, 1 \rangle$. Естественно, модель достаточно задать с точностью до изоморфизма. В этом смысле природа самих по себе чисел действительно не важна

Yarkin в сообщении #232325 писал(а):

Профессор Снэйп в сообщении #231342 писал(а):

Арифметика --- это наука о свойствах модели

Интересно, что Вы подразумеваете под моделью?

Профессор Снэйп кортеж нарисовал!
И другие так делают:
Кейслер Г. Дж., Чэн Ч.Ч. Теория моделей.
М.: Мир, 1977, сc. 52 — 65:
http://www.px-pict.com/9/6/2/4/3/1/2.html

Поэтому в качестве первого шага к определению понятия “модель” можно дать следующее: “Модель – это кортеж определенного вида”. Естественно, сразу же возникает вопрос (раз мы свели понятие “модели” к понятию “кортежа”): “А что такое кортеж?”

Ну, кортеж – это одно из основовных понятий теоретико-множественной математики. Причем в наших рассмотрениях мы вполне можем ограничиться ее “наивной” ветвью. Ведь даже матлогики постоянно так делают. Те же Кейслер с Чэном:
http://www.px-pict.com/9/6/2/4/3/1/3.html

Информация о кортежах в рамках “наивной’ теории множеств:
http://www.px-pict.com/9/1.html#5
В англоязычной литературе “кортеж” часто называется "tuple":
http://en.wikipedia.org/wiki/Tuple