Условная независимость относительно алгебр, теорвер

[id]

Определение:
Будем говорить, что $\sigma$-алгебры $\mathcal{G}_1$ и $\mathcal{G}_2$ условно независимы относительно $\sigma$-алгебры $\mathcal{G}_3$, если $\forall$ $A_i \in \mathcal{G}_i, i=1,2$ $P(A_1 A_2 | \mathcal{G}_3) = P(A_1 | \mathcal{G}_3) P(A_2 | \mathcal{G}_3)$, где $P(A | \mathcal{G}) = E( I_A | \mathcal{G})$ ( т.е. обычное УМО от индикатора $A$)

Показать, что это эквивалентно тому, что
$\forall A_1 \in \mathcal{G}_1$
$P (A_1 | \sigma(\mathcal{G}_2 \bigcup \mathcal{G}_3)) = P(A_1 | \mathcal{G}_3)$


В каком направлении подумать?
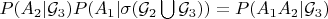
В одну сторону - пробовал из первого выразить $P(A_1 | \mathcal{G}_3)$, подставить во второе, чтобы получить тождество, но получилось выражение $P(A_2 | \mathcal{G}_3)P(A_1 | \sigma(\mathcal{G}_2 \bigcup \mathcal{G}_3)) = P(A_1 A_2 | \mathcal{G}_3)$, доказать которое пока не выходит. В другую не думаю, что будет лучше.

[Хорхе]

Необходимость: Возьмите $A\in\mathcal G_1, B\in \mathcal G_2$ и докажите, что
$P(A\cap B) = E(P(A|\mathcal G_3) I_B)$.

-- Сб июн 27, 2009 12:48:35 --

Достаточность вообще по определению.

[id]

Хм, не получается. Если кратко, как это доказывать? И как потом применить в док-ве необходимости?
И как по определению получается достаточность? ( хотя бы примерно )

[id]

Ну то есть для док-ва первой формулы пробовал от исходного взять матожидание, чтобы осталась слева нужная вероятность, так справа не получается ничего вынести. Использовать теоремы о равенстве измеримых функций относительно одной и той же алгебры при равенстве интегралов по множествам из нее - что-то тоже. Опять таки, как решать дальше - тоже не совсем представляю.

[Хорхе]

На всякий случай пишу определение:
$E(\xi|\mathcal F)$ -- это такая $\mathcal F$-измеримая величина $\eta$, что $E(I_A \xi) = E(I_A \eta)$ для всех $A\in \mathcal F$.

[id]

Хорхе
Спасибо, немного яснее. Подставляем индикаторы, получаем как раз формулу $P(A\cap B) = E(P(A|\mathcal G_3) I_B)$.

Хотя нет, не совсем получается, тут же нужно чтобы $A$ ( ну то есть $B$ в самое формуле ) было из $\mathcal{G}_3$. То есть получается не нужное $P(A\cap B) = E(P(A|\mathcal G_3) I_B)$, а ненужное $P(A\cap B) = E(P(A|\mathcal G_2) I_B)$

[Хорхе]

Из той формулы, что я написал в "необходимости" через метод подходящих множеств она распространяется на $B\in\sigma(\mathcal{G}_2 \cup \mathcal{G}_3)$, откуда следует, что $P(A_1 | \mathcal{G}_3)$ является $P (A_1 | \sigma(\mathcal{G}_2 \cup \mathcal{G}_3))$ именно по определению.

[id]

Хорхе
Из $P(A\cap B) = E(P(A|\mathcal G_3) I_B)$? С методом п.м. разберусь, но как саму формулу показать? Из определения ( выше написал ) вроде не выходит.

[Хорхе]

Ну есть же простая формула (которая тоже следует из определения )

$$ E(P(A|\mathcal G_3)I_B) = E\big[P(A|\mathcal G_3)P(B|\mathcal G_3)\big]. $$

[id]

Так, ну да, берем от $P(A|\mathcal G_3)I_B$ УМО по $\mathcal G_3$, интегрируем по всему пространству в определении, получается формула.

-- Вс июн 28, 2009 14:40:39 --

Далее, справа подставляем данное изначально, получаем ту самую формулу $P(A\cap B) = E(P(A|\mathcal G_3) I_B)$, из которой и с помощью $P(A\cap B) = E(P(A|\mathcal G_2) I_B)$ методом п.м. получаем $\forall A_1 \in \mathcal{G}_1$
$P (A_1 | \sigma(\mathcal{G}_2 \bigcup \mathcal{G}_3)) = P(A_1 | \mathcal{G}_3)$?

[Хорхе]

Ну да. Это необходимость

Теперь достаточность.

-- Вс июн 28, 2009 14:49:47 --

Кстати, достаточность гораздо быстрее получится не из определения, а из телескопического свойства (=теорема про три перпендикуляра).

[id]

Так, а первое телескопическое свойство или второе? И куда его примерно приткнуть?

[Хорхе]

Не знаю, первое или второе, но это где мы сначала проецируем на большую $\sigma$-алгебру, потом на меньшую. И приткнуть его к левой части равенства, которое нужно получить.

[id]

Хорхе
Да, все получилось.
$E(I_{A_1} I_{A_2} | \mathcal G_3) = E[ E( I_{A_1} I_{A_2}| \sigma(\mathcal G_2 \bigcup \mathcal G_3))| \mathcal G_3] = E[ I_{A_2} E( I_{A_1}| \sigma(\mathcal G_2 \bigcup \mathcal G_3))| \mathcal G_3] = E[ I_{A_2} E( I_{A_1}| \mathcal G_3)| \mathcal G_3] = E( I_{A_1}| \mathcal G_3) E( I_{A_2}| \mathcal G_3) $

Большое спасибо!