При

существует 6 правильных тел с символами Шлефли {3,3,3} (симплекс), {4,3,3} (гиперкуб), {3,3,4}, {3,4,3}, {5,3,3}, {3,3,5} (эти, по-моему, называются по числу граней; если хотите, сейчас поищу точную информацию о них). При
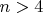
существуют только симплекс {3,3,...,3}, куб (точнее, гиперкуб) {4,3,...,3} и "гипероктаэдр" {3,3,...,4}. Как доказывается - точно не знаю, но все правильные тела как-то связаны с т.н. графом Кокстера (понятие не имею, что это такое), точнее, этот граф позволяет как-то выделить из всех мыслимых символов Шлефли символы правильных многогранников.