Кто-нибуть, может дать внятное объяснение, почему
![$F \left [ f \left ( t+t_0 \right) \right ] = \int\limits_{- \infty}^{+ \infty} f (t+t_0) e^{-i \omega t} dt$ $F \left [ f \left ( t+t_0 \right) \right ] = \int\limits_{- \infty}^{+ \infty} f (t+t_0) e^{-i \omega t} dt$](https://dxdy-04.korotkov.co.uk/f/f/1/e/f1e78345df57db2db182fabe5c6e2d2e82.png)
Ведь, по определению, преобразование Fourier записывается как
![$F \left [ f (t) \right ] = \int\limits_{- \infty}^{+ \infty} f (t) e^{-i \omega t} dt$ $F \left [ f (t) \right ] = \int\limits_{- \infty}^{+ \infty} f (t) e^{-i \omega t} dt$](https://dxdy-03.korotkov.co.uk/f/6/5/c/65c78bf5c2eec5368a53525c2e00b55b82.png)
Тогда, раз уж мы подстваляем вместо
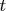

, тогда надо подствалять везде. В том числе и в показателе степени экспоненты. Т.е. я говорю об
![$F \left [ f \left ( t+t_0 \right) \right ] = \int\limits_{- \infty}^{+ \infty} f (t+t_0) e^{-i \omega (t+t_0)} dt$ $F \left [ f \left ( t+t_0 \right) \right ] = \int\limits_{- \infty}^{+ \infty} f (t+t_0) e^{-i \omega (t+t_0)} dt$](https://dxdy-01.korotkov.co.uk/f/8/3/7/837c1d231ff77a611e99c5b53204e24e82.png)
???
Это используется для доказательства следующего свойства преобразование Fourier :
![$F \left [ f(t+t_0) \right ] = e^{i \omega t_0} F \left [ f(t) \right ]$ $F \left [ f(t+t_0) \right ] = e^{i \omega t_0} F \left [ f(t) \right ]$](https://dxdy-04.korotkov.co.uk/f/b/0/7/b073ba6303e00f24bd9a8fc038ce48ca82.png)
.