Взял вот такой пример:
Условия:




. Решение выполнить с шагом

, определяя значения функции

с четырьмя десятичными знаками, причем
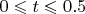
.
Пример:

Не могу подобрать сооотношение

, какое оно должно быть для неявной схемы??? Как я понял должна быть точка со следующего слоя. а вот составить немогу.