Найти все точки разрыва функции трех переменных.
u =

Что сделано:
Итак, знаменатель первой дроби обратится в ноль в тех точках, которые принадлежат сфере радиуса

с координатами центра
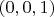
. Для краткости обозначим это множество точек

, а произвольные будем обозначать

.
1)

Предел в этих точках равен бесконечности, а значит это точки разрыва.
2)

Предел в этих точках равен нулю (знаменатель не обращается в ноль, а "е в степени" сремится к нулю). Функция в этих точках непрерывна.
3)

Отсюда следует, что этому условию удовлетворяет точка (0,0,0).
Здесь я впал в ступор, не могу найти предел в точке (0,0,0), а точнее - доказать что он равен нулю.
Не подскажете, что мне делать?