1. Необходимо проверить справедливость теоремы Лагранжа (о конечных приращениях) для функции

на отрезке [0;a] (a>0).
По теореме:


![$(c\in [0;a])$ $(c\in [0;a])$](https://dxdy-01.korotkov.co.uk/f/4/b/6/4b6fd46e75f329c100fca59f5ca46ed682.png)
подскажите, пожалуйста, что делать дальше..
2. Будет ли функция

дифференцируема в точке
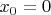
?
Я так понимаю, необходимо найти пределы слева и справа выражения

и сравнить... И оба предела получаются равны 0. Верно? Поэтому функция дифференцируема.