О невозможности КУБ представить суммой
двух кубов.
(второй вариант доказательства).
Рассмотрение свойств суммы двух чисел должно проводиться только для взаймно простых чисел. Это общеизвестно. Здесь будет идти речь о последовательных, или соседних числах, что означает, что числа находятся рядом в натуральном ряду чисел(7 , 8, 9…)
Разность кубов двух соседних чисел

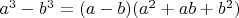
,

. Подставим

Задаемся вопросом: может ли полученная сумма двух чисел быть равна кубу?
Вспомним: любой куб всегда равен произведению трех последовательных чисел плюс среднее число

В полученной нами сумме есть произведение

. Изменяя

можно образовать произведение трех последовательных чисел. Два варианта:
Первый

, 1*2*3+1 среднее число =2
Второй

, 3*4*5+1 среднее число=4
Поскольку мы к произведению этих последовательных чисел прибавляем не 2 и не 4, то эти суммы кубу не равны.
И я полагаю очевидным, что при любых

больших 4, образовать здесь произведение трех последовательных чисел невазможно, да и 1 не есть среднее число. Поэтому зключаем, что разность кубов соседних чисел кубу равна быть не может.
А теперь перейдем к разности кубов двух любых (не соседних) чисел, но обязательно взаимно простых.
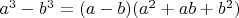
обозначим

. Подставим

Прдположим, что это число равно кубу. Тогда.

. Но слева есть множитель

, значит

Тогда

,

перенесем на право

. Посколко

и

, взаимно простые числа, то слева множителя

нет. Равенство не возможно. Поэтому

кубу не равно. Но Stop. Равенство

не исключается, если

. Но тогда разность кубов, как мы ее назвали любых (не соседних), будет разностью кубов соседних чисел, которая кубу не равна, что показано выше.
И так, разности кубов, соседних и любых кубу равны быть не могут. Куб не представим суммой двух кубов.
Petern1.