daogiauvang писал(а):
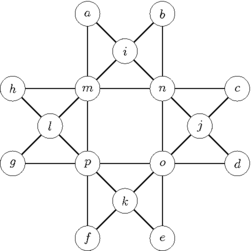
Сменить буква от a до p числами от 1 до 16 удовлетворяющие условиям: каждое число появляется один раз и суммы чисел каждой строки равны .
Каковы значения суммы чисел по строке???
Имеем:

чисел 1-го вида, присутствует в

строках 1-го и в

суммах 2-го вида (пусть сумма этих чисел

),

чисел 2-го вида, присутствует в

строках 1-го и в

суммах 2-го вида (пусть сумма этих чисел

) и

чисел 3-го вида, присутствует в

строках 1-го и в

суммах 2-го вида (пусть сумма этих чисел

).
Всего чисел по схеме

.
Общая сумма всех чисел по условию

.
Cумма строки 1-го вида состоит из

-х чисел 1-го,

-х чисел 2-го и

-го числа 3-го вида и равна

, а
сумма строки 2-го вида состоит из

-х чисел 1-го,

чисел 2-го и

числа 3-го вида и равна

.
По условию суммы строк всех видов равны:

.
Всего имеется

строки 1-го вида и

строки 2-го вида.
Сумма всех сумм строк 1-го вида состоит из

-х чисел 1-го,

-х чисел 2-го и

-го числа 3-го вида и равна

- причем, числа одного вида встречаются в ней одинаковое число раз (в силу транзитивной симметрии схемы), а именно, числа

-го вида

и, значит

.
Сумма всех сумм строк 2-го вида состоит из

-х чисел 1-го,

-х чисел 2-го и

-го числа 3-го вида и равна

- причем, числа одного вида встречаются в ней одинаковое число раз, а именно, числа

-вида

и, значит

.
Система структурных уравнений:

или

.
Итак, соображения симметрии приводят к 4-ем уравнениям от пяти неизвестных

,

,

,

,

.
Решения можно выразить через одну из неизвестных величин, например, сумму строки

:

.
Большего, увы, нам не дано.
Добавлено спустя 1 час 10 минут 11 секунд:
Наверно, нужно искать ограничения на

, исходя из данного набора чисел

..

.
Очень грубая оценка:
Максимальная сумма из 4-х чисел 2-го и 3-го вида равна

, а минимальная

, откуда

.
Сумма каждой из двух непересекающихся строк 1-го вида (по 5 элементов) не превышает
![$[(7+8+9+10+11+12+13+14+15+16)/2]=57$ $[(7+8+9+10+11+12+13+14+15+16)/2]=57$](https://dxdy-04.korotkov.co.uk/f/f/0/a/f0a7bab01f6204b49fd66536bace334982.png)
,
и не меньше
![$[(1+2+3+4+5+6+7+8+9+10)/2]_+=28$ $[(1+2+3+4+5+6+7+8+9+10)/2]_+=28$](https://dxdy-04.korotkov.co.uk/f/3/f/e/3fec6333b604b04e5f39de14e2a9314982.png)
, откуда

.
Максимальная сумма из 8-х чисел 1-го вида равна

, а минимальная

, откуда

.

или

(везде сужается оценка для

) или

или

или

.
Так как

и

, то заключаем, что

.
Больше времени нет думать.