Обобщенная специальная теория относительности.

[igorelki]

СТО – это частный случай данной теории, поэтому это не опровержение СТО.

Общие преобразования Лоренца используют математический аппарат, который опровергнуть невозможно. Если к ним добавить постулаты теории относительности и рассматривать пространство событий, описывающее физическое пространство, внутри всего светового конуса, то однозначно получаются коэффициенты преобразований из СТО. Если в пространстве событий рассмотреть поверхность светового (изотропного) конуса, то для этого подпространства можно ввести постоянный коэффициент для известных преобразований из СТО.
Можно рассмотреть вариант, когда СТО и сопутствующая СТО теория (ССТО) могут существовать одновременно.
Право на существование любых предложенных преобразований координат в пространстве Минковского – это:
1. существование инварианта двух точек, или неизменного интервала.
2. ортогональность предложенных преобразований.

(1. и 2. покажем при дальнейшем рассмотрении).

Изменение времени и расстояния обычного трехмерного пространства придвижении приводит нас к рассмотрению сигнала световых часов. Это означает, что мы рассматриваем событие прихода светового сигнала на зеркало и отправление сигнала от зеркала . Это означает, что информация об этих событиях могла быть доставлена только световым сигналом, что соответствует поверхности светового конуса.
Так как мы рассматриваем движение тела относительно наблюдателя, то приближение или удаление тела, движение трансверсально, будут восприниматься разными наблюдателями по-разному. Поэтому наблюдатели находятся не в одинаковых условиях. При этом один наблюдатель видит одни размеры движущегося тела, другой другие. Ведь никого не удивляет разница звука приближающегося и удаляющегося поезда – разная длина волны звука у одного поезда.
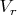
Рассмотрение движения световых часов приводит к изучению расстояния между часами и наблюдателем или к полярным координатам. При движении тела в полярных координатах известны две скорости $V_r$ и $V_\beta$. Основное требование при таком рассмотрении – это сохранение пути сигнала в световых часах при разных положениях часов.
Запишем эти скорости в Декартовых координатах. При прямолинейном движении всегда ось $x$ можно направить параллельно прямой движения, значит координата $y$ у нас не меняется. Тогда:
$V_r =\frac{dr}{dt}=\frac{Wx}{\sqrt{y^2+x^2}}$ (1)
$V_\beta=\frac{rd\beta}{dt}=\frac{rd(\arctg\frac{y}{x})}{dt}=\frac{Wy}{\sqrt {x^2+y^2}}$
Где
$W=\frac{dx}{dt}$
В пространстве событий на световом конусе преобразования координат Лоренца могут быть изменены на постоянный множитель $J$ см. http://ielkin1.livejournal.com/ :

$x=\frac{J(x^1+Vt^1)}{\sqrt{1-\frac{V^2}{c^2}}}$ (2)
$t=\frac{J(t^1+x^1\frac{V}{c^2})}{\sqrt{1-(\frac{V^2}{c^2})}}$
$y=Jy^1$, $z=Jz^1$,
где
$J=\frac{\sqrt{1-\frac{V^2}{c^2}}}{(1-\frac{V_r}{c})\sqrt{1-\frac{ V_\beta ^2}{c^2}}}$
$V=\sqrt {V_r^2+V_\beta ^2}$ – модуль скорости.
Получили преобразования:
x=$\frac{(x^1+Vt^1)}{(1-\frac{V_r}{c})(\sqrt{1-\frac{V_\beta ^2}{c^2}})}$ (3)
t=$\frac{(t^1+x^1\frac{V}{c^2})}{(1-\frac{V_r}{c})\sqrt {1-\frac{ V_\beta ^2}{c^2}}}$
y=$\frac{y^1\sqrt{1-\frac{V^2}{c^2}}}{(1-\frac{V_r}{c})\sqrt{1-\frac{ V_\beta ^2}{c^2}}}$
z=$\frac{z^1\sqrt{1-\frac{V^2}{c^2}}}{(1-\frac{V_r}{c})\sqrt {1-\frac{ V_\beta ^2}{c^2}}}$

Вернемся к вопросу об ортогональности преобразований (3) и наличии инварианта – интервала на поверхности изотропного конуса.
1. В случае преобразований (3) постоянный множитель $J$ может быть вынесен за скобку при вычислении интервала, в скобках остается вычисленный по СТО интервал, который на поверхности изотропного конуса =0. Следовательно, интервал в нашем случае с любой системе координат =0.
2. Ортогональность преобразований доказывается похожим способом на сайте http://ielkin1.livejournal.com/ .

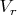
Ясно, что при координате $x$<<$y$ или при совпадении оси $y$ с осью $y^1$ расстояние не меняется, поэтому $V_r$ =0 и все формулы переходят в известные преобразования Лоренца для СТО, с известными выводами.

x=$\frac{(x^1+Vt^1)}{\sqrt{1-\frac{V^2}{c^2}}}$ (4)
t=$\frac{(t^1+x^1\frac{V}{c^2})}{\sqrt{1-\frac{V^2}{c^2}}}$
$y=y^1$, $z=z^1$,
При совпадении оси $x$ и оси $x^1$ или при $y$<<$ x$ угол не меняется, поэтому можно считать $ V_\beta $ =0 и преобразования координат будут из ССТО:

$x=\frac{(x^1+Vt^1)}{1-\frac{V}{c}}$ (5)
$t=\frac{(t^1+x^1\frac{V}{c^2})}{1-\frac{V}{c}}$
$y=\frac{y^1\sqrt{1+\frac{V}{c}}}{\sqrt{1-\frac{V}{c}}}$
$z=\frac{z^1\sqrt{1+\frac{V}{c}}}{\sqrt{1-\frac{V}{c}}}$
Обратные преобразования для (5) будут: решения уравнений(5) относительно штрихованных координат:

$x^1=\frac{(x-Vt)}{(1+\frac{V}{c})}$ (6)
$t^1=\frac{(t-x\frac{V}{c^2})}{1+\frac{V}{c}}$
$y^1=\frac{y\sqrt{1-\frac{V}{c}}}{\sqrt{1+\frac{V}{c}}}$
$z^1=\frac{z\sqrt{1-\frac{V}{c}}}{\sqrt{1+\frac{V}{c}}}$
Здесь рассматривается положительное значение $V= V_r$ – удаление.