Someone писал(а):
Комплексное число можно рассматривать как вектор на плоскости с декартовыми координатами

.
Т.е. для каждого комплексного числа

, которому можно поставить в соответствие вектор с началом в т.

( нач. координат) и концом в т.

, находится
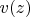
.
И для каждой точки

получаем некое другое комплексное число, которое в свою очередь также можно рассматривать как вектор на плоскости с декартовыми координатами?
и это будет векторное поле на комплексной плоскости?