Так как многочлен

неприводим над полем

, то если он не делит

, то эти многочлены взаимно-просты над

. В этом случае может существовать лишь конечное число простых

, по модулю которых эти многочлены не будут взаимно-просты.
Поясняю:
если

и

взаимно-просты над

, то существуют такие многочлены с целыми коэффициентами

и
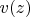
, что

где

- некоторое ненулевое целое число.
Рассматривая это равенство по модулю любого простого числа

, заключаем, что если

не делит

, то

и

являются взаимно простыми над

. Поэтому для того, чтобы

и

не были взаимно-просты над

,

обязано делить

. Но таких простых существует лишь конечное число.
Если уже доказали

над

, тем более это имеет место над С. Последнее означает, что для некоторых корней из 1

. А в этом случае очевидно (a,b,m)=(a,2a,3a).
Ну, конечно! Для этого достаточно записать корни

и

в комплексной форме и приравнять нулю действительную и мнимую часть...
Получается, что твоя задача полностью решена, хоть и с отрицательным ответом - искомых

не существует.



