Попытаюсь изменить вопрос:
Что нужно сделать для того чтобы найти динамическую ошибку данной САУ?
Ну. Я вам расскажду немного общей теории.
Для начала, я бы всю бурду из трех последовательных элементов свернул (я вообще не понял, зачем вы их сюда притащили) и получил бы систему с астатизмом 2го порядка и обратной связью. Ну пусть эквивалентная ПФ для последовательных трех элементов

(это вы сами посчитаете).
С учетом обратной связи у вас будет ПФ

(это вы тоже сами посчитаете, хотя я в уме все проделал).
На входе у вас сигнал

, где

- стационарный случайный сигнал, заданный спектральной плотностью

.
Значит, нам надо получить на выходе величину

или по формуле свертки

где

Ну на самом деле на выходе, конечно, никакой

не получится в силу разных ошибок, поэтому

где

- возмущающее воздействие.

- разумный предел (исходя из длительности ПП) времени случайного воздействия.
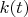
- импульсная переходная функция величины

.
Ошибка преобразования управляющего воздействия полезного сигнала

:

.
А динамическая ошибка (которая без случайных факторов):




