В какой из интервалов попадёт вероятность события

? (значок объединения не знаю, как поставить, но смысл ясен).

.
Я пробовал решать так. Вначале оценим

. О совместности или несовместности событий нам ничего неизвестно, поэтому:

Оценим вероятность произведения. События могут быть и зависимыми, поэтому:

Тогда

,
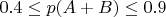
Подключая событие

и рассуждая аналогично, приходим к интервалу

Однако это не согласуется с ответом. Прошу указать на возможные огрехи решения!