arqady писал(а):
La|Verd писал(а):
2. Решить уравнение:
![$x=\sqrt[3]{3x-1}$ $x=\sqrt[3]{3x-1}$](https://dxdy-03.korotkov.co.uk/f/a/2/8/a289213b68b67018e0f0d53b28f5275b82.png)
Подстановка

дает все корни.

Будем считать, что кубический корень извлекается из любого действительного числа (по моему, это стандартное соглашение,

определено только при

, а
![$\sqrt[3]{x}$ $\sqrt[3]{x}$](https://dxdy-03.korotkov.co.uk/f/a/b/5/ab581c2338e8b905c9c807686656132982.png)
определено при всех действительных

). Это означает, что исходное уравнение равносильно уравнению

или

Подстановка

вместе с формулой

даёт

,

и

. Отсюда

и

. Теперь если ограничить

на полуинтервал

(нам ведь нужно только значение косинуса

), то получаем

Приняв во внимание чётность косинуса, выкидываем из этого множества отрицательные значения, которые по модулю совпадают с положительными. Остаётся

Небольшое упражнение с калькулятором даёт нам следующую информацию. Числа

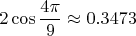

действительно являются корнями уравнения

. Таким образом, все три корня найдены и всё тип-топ.
Остаётся вопрос: нужно ли оставлять ответ в таком виде или эти косинусы надо вычислять в радикалах. Я не вижу, как можно перейти к радикалам, не используя формулы Кардано. С другой стороны, аргумент у каждого следующего косинуса вдвое больше аргумента предыдущего, так что достаточно вычислить один косинус, а затем работать с формулой косинуса удвоенного угла.