Как быстро разожмётся отпущенная пружина?

[Kosmos]

Как быстро разожмётся отпущенная пружина?

То есть, если её сжать, а потом мгновенно отпустить. При этом никакой нагрузки на ней нет. С какой в результате скоростью она будет разжиматься?

[Zai]

Пружина является балкой, работающей на кручение. У ней есть собственные частоты и формы колебаний. В момент, когда она стала свободной, моды колебаний возбуждаются. Большая часть энергии сжатия переходит в первую форму колебаний с наименьшей частотой. Можно предположить, что за четверть периода этой формы колебаний пружина будет иметь наименьшую потенциальную энергию, т.е. разожмется, хотя в ней будет еще много кинетической энергии. Последующие колебания с затуханием (около 20 периодов первой формы колебаний) приведут к относительно полной диссипации энергии сжатия (свыше 95%).

[Kosmos]

Zai писал(а):

Пружина является балкой, работающей на кручение. У ней есть собственные частоты и формы колебаний. В момент, когда она стала свободной, моды колебаний возбуждаются. Большая часть энергии сжатия переходит в первую форму колебаний с наименьшей частотой. Можно предположить, что за четверть периода этой формы колебаний пружина будет иметь наименьшую потенциальную энергию, т.е. разожмется, хотя в ней будет еще много кинетической энергии. Последующие колебания с затуханием (около 20 периодов первой формы колебаний) приведут к относительно полной диссипации энергии сжатия (свыше 95%).

А эти частоты и формы колебаний можно рассчитать?

[alexrey036]

Kosmos писал(а):

Как быстро разожмётся отпущенная пружина?

То есть, если её сжать, а потом мгновенно отпустить. При этом никакой нагрузки на ней нет. С какой в результате скоростью она будет разжиматься?

Эта задача практически не отличается от школьной задачи нахождения периода колебаний (время разжатия - четверть периода) груза на пружинке. Только роль груза выполняет сама пружина (груз не сосредоточен, а распределен).

[Zai]

Kosmos писал(а):

А эти частоты и формы колебаний можно рассчитать?

Не думаю что это сложно сделать в пакетах МКЭ. См. http://e-strength.ru/mydemo.files/frame.htm
Слайд 19 - деформация пружины.

[Kosmos]

alexrey036 писал(а):

Kosmos писал(а):

Как быстро разожмётся отпущенная пружина?

То есть, если её сжать, а потом мгновенно отпустить. При этом никакой нагрузки на ней нет. С какой в результате скоростью она будет разжиматься?

Эта задача практически не отличается от школьной задачи нахождения периода колебаний (время разжатия - четверть периода) груза на пружинке. Только роль груза выполняет сама пружина (груз не сосредоточен, а распределен).

А можно ссылку на практическое решение этой задачи для какого-нибудь реального материала пружины?

[Zai]

Kosmos писал(а):

А можно ссылку на практическое решение этой задачи для какого-нибудь реального материала пружины?

Время четверть периода приближенно можно оценить по следующим формулам:
$ \omega_1=\sqrt{\frac {3K} {m}}
$ T=2\pi \sqrt{\frac {m} {3K}}
Время разжатия по первой форме колебаний
$ T_1=\frac T 4=\frac {\pi} 2 \sqrt{\frac {m} {3K}}
$ {m} - масса пружины, кг
$ {K} - линейная жесткость пружины, н/м

[Kosmos]

Zai писал(а):

Kosmos писал(а):

А можно ссылку на практическое решение этой задачи для какого-нибудь реального материала пружины?

Время четверть периода приближенно можно оценить по следующим формулам:
$ \omega_1=\sqrt{\frac {3K} {m}}
$ T=2\pi \sqrt{\frac {m} {3K}}
Время разжатия по первой форме колебаний
$ T_1=\frac T 4=\frac {\pi} 2 \sqrt{\frac {m} {3K}}
$ {m} - масса пружины, кг
$ {K} - линейная жесткость пружины, н/м

А чему равна реальная линейная жёсткость пружины для какого-нибудь реального материала?

Мне бы какой-нибудь интернет-справочник, где бы были описаны жёсткости пружин из разных реальных материалов. А то нигде найти не могу. Поэтому даже порядок цифр не представляю.

[Andrei P]

Kosmos писал(а):

alexrey036 писал(а):

Kosmos писал(а):

Как быстро разожмётся отпущенная пружина?

То есть, если её сжать, а потом мгновенно отпустить. При этом никакой нагрузки на ней нет. С какой в результате скоростью она будет разжиматься?

Эта задача практически не отличается от школьной задачи нахождения периода колебаний (время разжатия - четверть периода) груза на пружинке. Только роль груза выполняет сама пружина (груз не сосредоточен, а распределен).

А можно ссылку на практическое решение этой задачи для какого-нибудь реального материала пружины?

Практически, в первом приближении, можно взять основную частоту продольных колебаний по модели эквивалентного бруса (пружина заменяется прямым стержнем с аналогичной жесткостью, длиной и т.д.):
$ p_0 = 1/i \sqrt{ \frac{g }{\gamma} \frac{Gd^2}{2D^4}} $
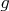
где $ i $ - количество рабочих витков, $ g $ = 9,8 м/с^2, $ G $ - модуль сдвига (характеристика упругости материала), $ d $ - диаметр прутка, $ D $- средний диаметр пружины, $ \gamma $ -- плотность материала.

Эта величина мало зависит от граничных условий. То, что большая часть энергии перейдет в "первую" моду --- не факт. Формула точнее для длинных пружин.

Не рекомендую использовать МКЭ по следующим причинам:

1. Легко наломать дров и получить неверный результат. Сложный частотный спектр и не всегда модель будет адекватной. Я видел решения МКЭ с частотами, которых нет и быть не может.

2. Сложный частотный спектр. Для длинных пружин наименьшая частота -- осн. частота пространственных поперечных колебаний. Для коротких -- осн. частота пространственных продольных колебаний. Разобраться без личного опыта затруднительно. Большая часть частот зависит от граничных условий и от поджатия. Здесь проблема интерпретации результата.

Кстати, не уверен, что Ваше решение работает всегда. Навскидку, если пружина теряет устойчивость. Для чего задача, если не секрет.

Если интересно, мог бы выложить график частотного спектра при порождающем решении. Если разберусь, как цеплять здесь картинки, ну и если народу интересно.

Добавлено спустя 9 минут 41 секунду:

Kosmos писал(а):

А чему равна реальная линейная жёсткость пружины для какого-нибудь реального материала?

Берем учебник по сопромату, выводим через интеграл Мора, у Феодосьева есть формула с выводом, учебник есть в интернете.
Справочники типа -- Пономарев С.Д. Андреева Л.Е. Расчет упругих элементов машин и приборов.
Привожу оттуда $ Z = \frac{Gd^4}{8D^3 i} $
Обозначения см. выше.