Теорема Колмогорова и Хинчина о двух рядах

[ihq.pl]

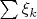
Вернее, часть этой теоремы: пусть $\xi_1,\xi_2,...$ -- последовательность независимых с.в. Для сходимости с вероятностью единица ряда $\sum \xi_k$ достаточно, чтобы одновременно сходились ряды $\sum \mathsf{D}\xi_n$ и $\sum\mathsf{E}\xi_n$.

Док-во. Если сходится ряд $\sum\mathsf{D}\xi_n$, то сходится и ряд $\sum (\xi_n-\mathsf{E}\xi_n)$. Но по предположению ряд $\mathsf{E}\xi_n$ сходится, поэтому сходится и ряд $\sum\xi_n$.

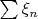
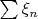
У меня получилось, что для сходимости $\sum\xi_n$ достаточно, чтобы сходился лишь один ряд $\sum\mathsf{D}\xi_n$.
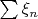
Пусть $\sum \mathsf{D}\xi_n = C$, и $M=\sqrt{2C}$. Допустим, ряд $\sum \xi_n$ расходится. Для каждого $k\in\mathbb{N}$ положим

$$A_k = \{|\xi_1+...+\xi_k| \geqslant M\}.$$

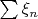
Из закона "0 или 1" Колмогорова ряд $\sum \xi_n$ расходится с вероятностью единица. Поэтому $\mathsf{P}(A_k)\to 1,\; k\to\infty$, т.е. для любого $\varepsilon>0$ найдется $N$ такое, что

$$\mathsf{P}(A_k) \geqslant 1-\varepsilon,\quad k\geqslant N\eqno{(1)}$$

Но из неравенства Чебышева вытекает, что

$$\mathsf{P}(A_k)\leqslant \frac{1}{M^2}\sum_{n=1}^k \mathsf{D}\xi_n \leqslant \frac{C}{M^2} = 1/2,$$

что противоречит $(1)$. Это верно?

[mihaild]

ihq.pl в сообщении #1686008 писал(а):

$\mathsf{P}(A_k)\leqslant \frac{1}{M^2}\sum_{n=1}^k \mathsf{D}\xi_n$

Это почему? В неравенстве Чебышева еще мат. ожидание есть.
Рассмотрите простейший контрпример: $\xi_1 = 1$ п.н.

(кстати, из того, что ряд расходится, не следует неограниченность частичных сумм по модулю, но это другой вопрос)

[ihq.pl]

mihaild в сообщении #1686010 писал(а):

Это почему? В неравенстве Чебышева еще мат. ожидание есть.

Понял. Спасибо! Пропустил. Интуитивно тоже должно быть понятно, что сходимости ряда из дисперсий не достаточно.

-- 16.05.2025, 13:25 --

mihaild в сообщении #1686010 писал(а):

(кстати, из того, что ряд расходится, не следует неограниченность частичных сумм по модулю, но это другой вопрос)

Об этом тоже не подумал. Ужс