=============================================================
Number of points: 6
Number of hard edges: 12
Minimal distance: 1.41421356237309
Spherical distance: 90 deg
Coordinates:
0.816496580927726 0 0.577350269189626
-0.408248290463863 0.707106781186548 0.577350269189626
-0.408248290463863 -0.707106781186548 0.577350269189626
0.408248290463863 0.707106781186547 -0.577350269189626
0.408248290463863 -0.707106781186547 -0.577350269189626
-0.816496580927726 0.000000000000000 -0.577350269189626
=============================================================
Number of points: 7
Number of hard edges: 12
Minimal distance: 1.25687046848066
Spherical distance: 77.8695421554234 deg
Coordinates:
0.725654503313800 0 0.688059257491971
-0.362827251656900 0.628435234240330 0.688059257491971
-0.362827251656900 -0.628435234240330 0.688059257491971
0.488835833773143 0.846688500655378 -0.210138312730603
0.488835833773143 -0.846688500655378 -0.210138312730603
-0.977671667546286 0.000000000000000 -0.210138312730603
0.000000000000000 0 -1.000000000000000
=============================================================
Number of points: 8
Number of hard edges: 16
Minimal distance: 1.21556252413132
Spherical distance: 74.8584921856155 deg
Coordinates:
0.859532503769496 0 0.511081084529394
0.000000000000000 0.859532503769496 0.511081084529394
0.000000000000000 -0.859532503769496 0.511081084529394
-0.859532503769496 0.000000000000000 0.511081084529394
0.607781262065662 0.607781262065662 -0.511081084529394
0.607781262065662 -0.607781262065662 -0.511081084529394
-0.607781262065662 0.607781262065662 -0.511081084529394
-0.607781262065662 -0.607781262065662 -0.511081084529394
=============================================================
Number of points: 9
Number of hard edges: 18
Minimal distance: 1.15470053837925
Spherical distance: 70.5287793655093 deg
Coordinates:
0.666666666666667 0 0.745355992499930
-0.333333333333333 0.577350269189626 0.745355992499930
-0.333333333333333 -0.577350269189626 0.745355992499930
0.500000000000000 0.866025403784439 0.000000000000000
0.500000000000000 -0.866025403784439 0.000000000000000
-1.000000000000000 0.000000000000000 0.000000000000000
0.666666666666667 0 -0.745355992499930
-0.333333333333333 0.577350269189626 -0.745355992499930
-0.333333333333333 -0.577350269189626 -0.745355992499930
=============================================================
Number of points: 10
Number of hard edges: 19
Minimal distance: 1.09142629140382
Spherical distance: 66.1468219878905 deg
Coordinates:
0.000000000000000 0.609945710115265 0.792443203461286
0.000000000000000 -0.609945710115265 0.792443203461286
0.859988553050598 0 0.510313323970615
-0.859988553050598 0.000000000000000 0.510313323970615
0.545713145701910 0.828261362520315 -0.127201721545415
-0.545713145701910 0.828261362520315 -0.127201721545415
-0.545713145701910 -0.828261362520315 -0.127201721545415
0.545713145701910 -0.828261362520315 -0.127201721545415
0.545713145701911 0 -0.837972053596136
-0.545713145701911 0.000000000000000 -0.837972053596136
=============================================================
Number of points: 11
Number of hard edges: 25
Minimal distance: 1.05146222423827
Spherical distance: 63.434948822922 deg
Coordinates:
0.894427190999916 0 0.447213595499958
0.276393202250021 0.850650808352040 0.447213595499958
0.276393202250021 -0.850650808352040 0.447213595499958
-0.723606797749979 0.525731112119134 0.447213595499958
-0.723606797749979 -0.525731112119134 0.447213595499958
0.723606797749979 0.525731112119134 -0.447213595499958
0.723606797749979 -0.525731112119134 -0.447213595499958
-0.276393202250021 0.850650808352040 -0.447213595499958
-0.276393202250021 -0.850650808352040 -0.447213595499958
-0.894427190999916 0.000000000000000 -0.447213595499958
0.000000000000000 0 -1.000000000000000
=============================================================
Number of points: 12
Number of hard edges: 30
Minimal distance: 1.05146222423827
Spherical distance: 63.434948822922 deg
Coordinates:
0 0 1.000000000000000
0.894427190999916 0 0.447213595499958
0.276393202250021 0.850650808352040 0.447213595499958
0.276393202250021 -0.850650808352040 0.447213595499958
-0.723606797749979 0.525731112119134 0.447213595499958
-0.723606797749979 -0.525731112119134 0.447213595499958
0.723606797749979 0.525731112119134 -0.447213595499958
0.723606797749979 -0.525731112119134 -0.447213595499958
-0.276393202250021 0.850650808352040 -0.447213595499958
-0.276393202250021 -0.850650808352040 -0.447213595499958
-0.894427190999916 0.000000000000000 -0.447213595499958
0.000000000000000 0 -1.000000000000000
=============================================================
Number of points: 13
Number of hard edges: 24
Minimal distance: 0.956413627224499
Spherical distance: 57.1367030775783 deg
Coordinates:
0.676286561429666 0 0.736638640603138
0.000000000000000 0.676286561429666 0.736638640603138
0.000000000000000 -0.676286561429666 0.736638640603138
-0.676286561429666 0.000000000000000 0.736638640603138
0.704230456710091 0.704230456710091 0.090105092440959
0.704230456710091 -0.704230456710091 0.090105092440959
-0.704230456710091 0.704230456710091 0.090105092440959
-0.704230456710091 -0.704230456710091 0.090105092440959
0.839967644115645 0 -0.542636486829639
0.000000000000000 0.839967644115645 -0.542636486829639
0.000000000000000 -0.839967644115645 -0.542636486829639
-0.839967644115645 0.000000000000000 -0.542636486829639
0.000000000000000 0 -1.000000000000000
=============================================================
Number of points: 14
Number of hard edges: 28
Minimal distance: 0.933862623344028
Spherical distance: 55.6705699956595 deg
Coordinates:
0 0 1.000000000000000
0.681127894674377 0.466931311672014 0.563950300360505
0.681127894674377 -0.466931311672014 0.563950300360505
-0.681127894674377 -0.466931311672014 0.563950300360505
-0.681127894674376 0.466931311672014 0.563950300360505
0.000000000000000 0.982441144573429 0.186572767169410
0.000000000000000 -0.982441144573429 0.186572767169410
0.982441144573429 0 -0.186572767169410
-0.982441144573429 0.000000000000000 -0.186572767169410
-0.466931311672014 0.681127894674376 -0.563950300360505
0.466931311672014 0.681127894674377 -0.563950300360505
0.466931311672014 -0.681127894674377 -0.563950300360505
-0.466931311672014 -0.681127894674376 -0.563950300360505
0.000000000000000 0 -1.000000000000000
=============================================================
Number of points: 15
Number of hard edges: 30
Minimal distance: 0.902656188229966
Spherical distance: 53.6578501299326 deg
Coordinates:
0.260574396630126 0.451328094114983 0.853465837209306
0.260574396630126 -0.451328094114983 0.853465837209306
-0.521148793260253 0.000000000000000 0.853465837209306
0.908985923112752 0 0.416826812456754
-0.454492961556376 0.787204901098092 0.416826812456754
-0.454492961556376 -0.787204901098092 0.416826812456754
0.376835267797373 0.921711972287309 0.091881560099513
0.609808349074382 -0.787204901098091 0.091881560099513
-0.965392708383380 -0.244079285302712 -0.091881560099513
0.843082907030753 0.339803796755889 -0.416826812456754
-0.715820173808380 0.560229316607122 -0.416826812456754
-0.127262733222372 -0.900033113363010 -0.416826812456754
0.072963527992517 0.516015879890826 -0.853465837209306
0.410401096745376 -0.321196208736669 -0.853465837209306
-0.483364624737893 -0.194819671154156 -0.853465837209306
=============================================================
Number of points: 16
Number of hard edges: 32
Minimal distance: 0.880574112176032
Spherical distance: 52.2443957527206 deg
Coordinates:
0.622659926056996 0 0.782492566407309
0.000000000000000 0.622659926056996 0.782492566407309
0.000000000000000 -0.622659926056996 0.782492566407309
-0.622659926056996 0.000000000000000 0.782492566407309
0.687190046418906 0.687190046418906 0.235668581286442
0.687190046418906 -0.687190046418906 0.235668581286442
-0.687190046418906 0.687190046418906 0.235668581286442
-0.687190046418906 -0.687190046418906 0.235668581286442
0.971833483573413 0 -0.235668581286442
0.000000000000000 0.971833483573413 -0.235668581286442
0.000000000000000 -0.971833483573413 -0.235668581286442
-0.971833483573413 0.000000000000000 -0.235668581286442
0.440287056088016 0.440287056088016 -0.782492566407309
0.440287056088016 -0.440287056088016 -0.782492566407309
-0.440287056088016 0.440287056088016 -0.782492566407309
-0.440287056088016 -0.440287056088016 -0.782492566407309
=============================================================
Number of points: 17
Number of hard edges: 34
Minimal distance: 0.862444879316907
Spherical distance: 51.0903285516277 deg
Coordinates:
0.000000000000000 0.553910528530291 0.832576198544790
0.000000000000000 -0.553910528530291 0.832576198544790
0.656416466468028 0 0.754398715898713
-0.656416466468028 0.000000000000000 0.754398715898713
0.638757213967231 0.717900538765430 0.276781570999816
0.638757213967231 -0.717900538765430 0.276781570999816
-0.638757213967231 -0.717900538765430 0.276781570999816
-0.638757213967231 0.717900538765430 0.276781570999816
0.999317174356973 0 -0.036948410455591
-0.999317174356973 0.000000000000000 -0.036948410455591
0.000000000000000 0.969459500917063 -0.245251454800248
0.000000000000000 -0.969459500917063 -0.245251454800248
0.605300639615620 0.488987261018904 -0.628094415070021
0.605300639615620 -0.488987261018904 -0.628094415070021
-0.605300639615620 -0.488987261018904 -0.628094415070021
-0.605300639615620 0.488987261018904 -0.628094415070021
0.000000000000000 0 -1.000000000000000

 , которую будем максимизировать
, которую будем максимизировать  . При этом возникают ограничения в форме неравенств
. При этом возникают ограничения в форме неравенств  , где
, где  - квадрат расстояния между точками
- квадрат расстояния между точками  и
и  . Также должны быть выполнены ограничения в форме равенств
. Также должны быть выполнены ограничения в форме равенств  .
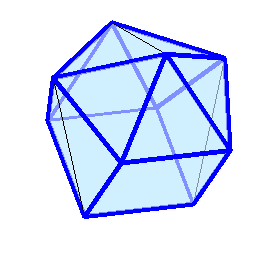
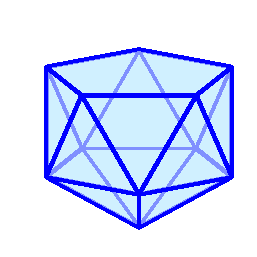
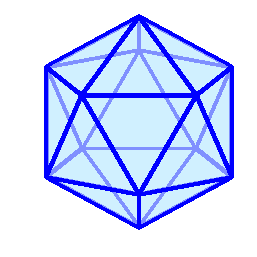
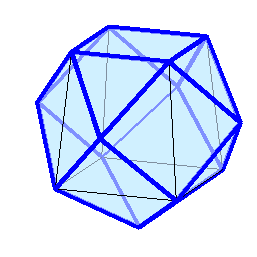
.  Визуализация этих многогранников ("толстые" рёбра синего цвета являются жёсткими) и точно рассчитанные (на сколько разрядность позволяет) координаты в конце под катом:
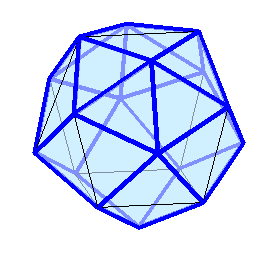
Визуализация этих многогранников ("толстые" рёбра синего цвета являются жёсткими) и точно рассчитанные (на сколько разрядность позволяет) координаты в конце под катом: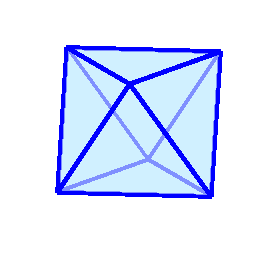
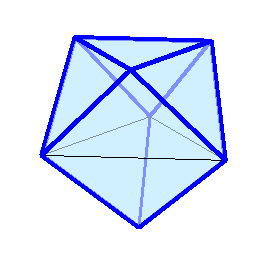
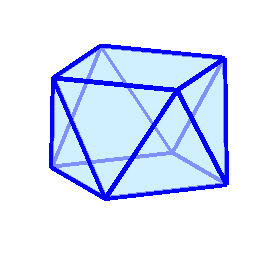

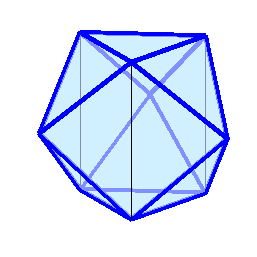
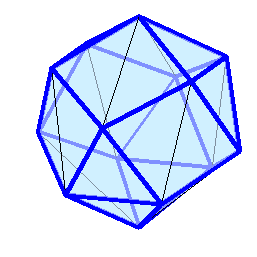
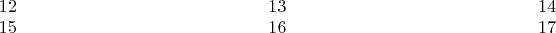
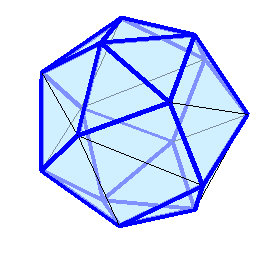
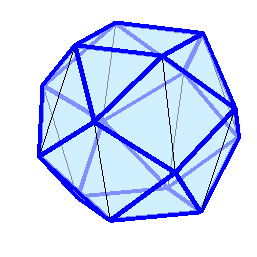
 ,
,  (максимизируется минимальное расстояние между точками
(максимизируется минимальное расстояние между точками  , потому что буква
, потому что буква  . А то будем путаться и других путать, обозначая разные вещи одной буквой.
. А то будем путаться и других путать, обозначая разные вещи одной буквой. где
где  а функция
а функция  Задача состоит в том, чтобы найти максимум целевой функции:
Задача состоит в том, чтобы найти максимум целевой функции:  которая равна
которая равна  Другими словами, нужно найти такое расположение точек на сфере, чтобы минимальное расстояние между любыми из возможных пар было максимально. Тут есть особые случаи, но пока забудем про них.
Другими словами, нужно найти такое расположение точек на сфере, чтобы минимальное расстояние между любыми из возможных пар было максимально. Тут есть особые случаи, но пока забудем про них.
 Некоторые нестрогие неравенства выше (уж точно по крайней мере одно) могут обратиться в равенства. Это будет происходить для пар вершин, соединённых жёсткими рёбрами. Обозначим их количество буквой
Некоторые нестрогие неравенства выше (уж точно по крайней мере одно) могут обратиться в равенства. Это будет происходить для пар вершин, соединённых жёсткими рёбрами. Обозначим их количество буквой  Выше все переменные
Выше все переменные 
 форму многогранника или нет?
форму многогранника или нет? Однако, это движение не может быть произвольным, поскольку, во-первых, точки лежат на сфере, поэтому на дифференциалы координат накладываются следствия этих ограничений:
Однако, это движение не может быть произвольным, поскольку, во-первых, точки лежат на сфере, поэтому на дифференциалы координат накладываются следствия этих ограничений:  Получается система из
Получается система из  где индекс
где индекс 


 Опять же, этот набор равенств можно записать через тензор третьего ранга или, как я делаю, в матричной форме:
Опять же, этот набор равенств можно записать через тензор третьего ранга или, как я делаю, в матричной форме:  Здесь индекс
Здесь индекс  Матрица
Матрица  Вместе со сферическим ограничением это приведёт к такой системе уравнений:
Вместе со сферическим ограничением это приведёт к такой системе уравнений:  И вот здесь уже видится что-то полезное. А именно, если некоторое жёсткое ребро является следствием наличия других рёбер и/или геометрии задачи, то соответствующая ему строка в полной матрице будет линейно выражаться через некоторый набор других строк. Это, в частности, позволяет установить, когда измерение длины одного жёсткого ребра неизбежно ведёт к изменению длины других жёстких рёбер, даже если многогранник не имеет фиксированной формы (в силу промежуточности решения). Конкретные тонкости этого вопроса для меня пока туманны.
И вот здесь уже видится что-то полезное. А именно, если некоторое жёсткое ребро является следствием наличия других рёбер и/или геометрии задачи, то соответствующая ему строка в полной матрице будет линейно выражаться через некоторый набор других строк. Это, в частности, позволяет установить, когда измерение длины одного жёсткого ребра неизбежно ведёт к изменению длины других жёстких рёбер, даже если многогранник не имеет фиксированной формы (в силу промежуточности решения). Конкретные тонкости этого вопроса для меня пока туманны. ранг её матрицы не может быть быть больше чем
ранг её матрицы не может быть быть больше чем  Это является следствием того, что вращательные степени свободы многогранника как целого не были зафиксированы уравнениями выше. Чтобы убить эти степени свободы можно сделать следующее. Построить аналог момента импульса рассматривая дифференциалы координат точек как компоненты их скоростей (квадратные скобки в формуле ниже означают векторное произведение):
Это является следствием того, что вращательные степени свободы многогранника как целого не были зафиксированы уравнениями выше. Чтобы убить эти степени свободы можно сделать следующее. Построить аналог момента импульса рассматривая дифференциалы координат точек как компоненты их скоростей (квадратные скобки в формуле ниже означают векторное произведение): ![$$d\mathbf{M}=\sum\limits_{n=1}^N\Bigl[\mathbf{R}\bigl(P,\;n\bigr),\;d\mathbf{R}\bigl(dP,\;n\bigr)\Bigr]$$ $$d\mathbf{M}=\sum\limits_{n=1}^N\Bigl[\mathbf{R}\bigl(P,\;n\bigr),\;d\mathbf{R}\bigl(dP,\;n\bigr)\Bigr]$$](https://dxdy-03.korotkov.co.uk/f/2/3/f/23fce96c0cf4706495905c2b0518495182.png) Приравнять нулю и записать это выражение в матричной форме:
Приравнять нулю и записать это выражение в матричной форме:  Здесь индекс
Здесь индекс  допускает ненулевое решение, то это означает, что существует движение точек (не являющееся тривиальным вращением многогранника как целого), которое сохраняет длины жёстких рёбер, но изменяет положение точек. Ненулевой вектор
допускает ненулевое решение, то это означает, что существует движение точек (не являющееся тривиальным вращением многогранника как целого), которое сохраняет длины жёстких рёбер, но изменяет положение точек. Ненулевой вектор  Подобное движение точек (сохраняющее длины жёстких рёбер) может быть необходимым промежуточным шагом, перед тем, как появится возможность сдвинуть точки так, что улучшится целевая функция.
Подобное движение точек (сохраняющее длины жёстких рёбер) может быть необходимым промежуточным шагом, перед тем, как появится возможность сдвинуть точки так, что улучшится целевая функция. при условии, что все компоненты дифференциала
при условии, что все компоненты дифференциала  и хотя бы один из них положителен? Ответ на этот вопрос осложняется тем, что система скорее всего переопределена и увеличение длины одного ребра с необходимостью приведёт к измерению длины других рёбер, в том числе к их уменьшению, что противоречит требованию задачи. Чтобы система оказалась разрешима необходимо выкинуть часть линейно зависимых уравнений, но это может привести к тому, что будет выкинуто то уравнение, которое соответствует уменьшающемуся при найденном движении ребру, это означает, что отброшена критическая информация. Видится возможность побороть эту проблему перебором, но в целом всё довольно туманно и вопрос эффективности такого подхода открыт (цэ из эн по ка и всё такое).
и хотя бы один из них положителен? Ответ на этот вопрос осложняется тем, что система скорее всего переопределена и увеличение длины одного ребра с необходимостью приведёт к измерению длины других рёбер, в том числе к их уменьшению, что противоречит требованию задачи. Чтобы система оказалась разрешима необходимо выкинуть часть линейно зависимых уравнений, но это может привести к тому, что будет выкинуто то уравнение, которое соответствует уменьшающемуся при найденном движении ребру, это означает, что отброшена критическая информация. Видится возможность побороть эту проблему перебором, но в целом всё довольно туманно и вопрос эффективности такого подхода открыт (цэ из эн по ка и всё такое). ищем ближайший сверху такой дополненно-раздутый, и ищем на сколько он отличается от того, что надо нам. Далее находим две параллели близкие по значению одну в северном, другую в южном полушариях, на которых в сумме будет столько точек, как если отнять числа точек в этом раздуто-дополненного икосаэдре значение
ищем ближайший сверху такой дополненно-раздутый, и ищем на сколько он отличается от того, что надо нам. Далее находим две параллели близкие по значению одну в северном, другую в южном полушариях, на которых в сумме будет столько точек, как если отнять числа точек в этом раздуто-дополненного икосаэдре значение 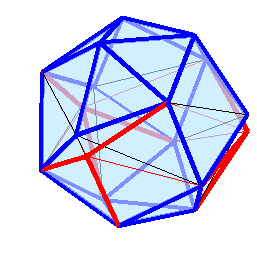

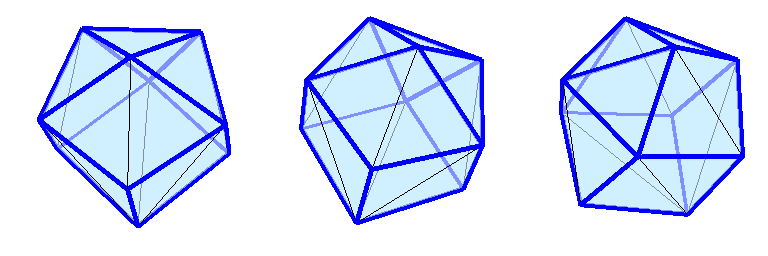
 а затем построить график зависимости длины оптимального ребра от параметра лямбда, то на нём будет два максимума:
а затем построить график зависимости длины оптимального ребра от параметра лямбда, то на нём будет два максимума: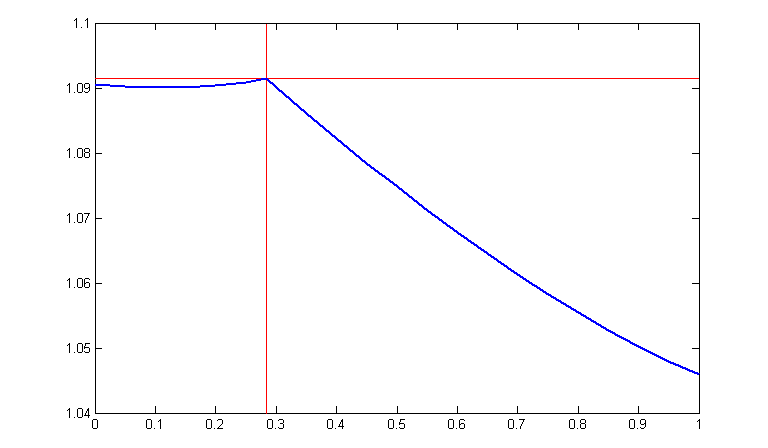
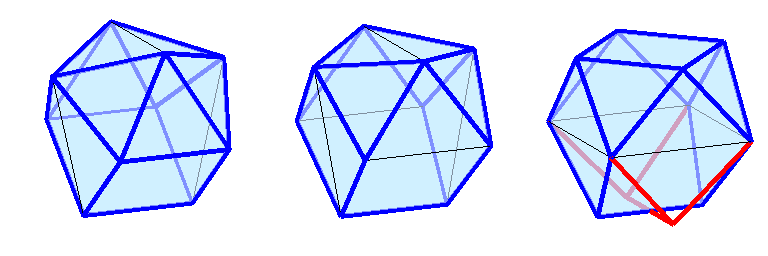
 раз длиннее оптимального, превратившись в диагональ квадратной грани, которая получается слиянием двух прилегающих треугольных граней. Это изображено на нижнем правом рисунке. Эта конфигурация не является не в каком смысле оптимальной (даже седловой), но она имеет одну замечательную особенность: пара самых нижних точек может быть расположена двояко и это не изменит целевую функцию задачи. На рисунке альтернативное расположение точек отмечено выходящими из них красными жёсткими рёбрами.
раз длиннее оптимального, превратившись в диагональ квадратной грани, которая получается слиянием двух прилегающих треугольных граней. Это изображено на нижнем правом рисунке. Эта конфигурация не является не в каком смысле оптимальной (даже седловой), но она имеет одну замечательную особенность: пара самых нижних точек может быть расположена двояко и это не изменит целевую функцию задачи. На рисунке альтернативное расположение точек отмечено выходящими из них красными жёсткими рёбрами.