Не могли бы вы привести пример данной линейной программы, чтобы было понятно, что вы имеете в виду.
Для ответа на Ваш вопрос воспользовался ИИ. Вот его ответ.
Для формализации задачи о нахождении минимальной суммы пути короля через таблицу 10×10 в рамках линейного программирования (ЛП) выполним следующие шаги:
1. Определение переменных:
- Бинарные переменные посещения клеток:

, если король посещает клетку

, и

в противном случае.
Всего:

переменных.
- Переменные переходов:

где

, если король перемещается из клетки

в

.
Всего:

переменных (каждая клетка имеет до 8 соседей).
2. Целевая функция:
Минимизировать общую сумму чисел на пути:
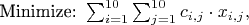
где

— число в клетке

.
3. Ограничения:
a) Старт и финиш:
- Король начинает в первом столбце:

- Король заканчивает в десятом столбце:

b) Последовательность пути:
- Единственность посещения:
Каждую клетку можно посетить не более одного раза:

- Связь переходов и посещений:
Если король переходит из

в

, то обе клетки должны быть посещены:

- Непрерывность пути:
Для каждой клетки

, кроме стартовой и конечной:

c) Допустимые переходы:
Переходы возможны только между соседними клетками (включая диагональ):

4. Проблемы модели:
- Вычислительная сложность: Модель содержит

переменных и

ограничений, что делает её решение трудоёмким даже для современных солверов.
- Целочисленность: Задача требует бинарных переменных, поэтому это целочисленное линейное программирование (ILP), которое NP-трудно.
Таким образом, задачу можно формально свести к ILP, но линейное программирование здесь используется как теоретический инструмент для формализации, а не для эффективного решения.
Другой подход сведения антагонистических игр к задаче линейного программирования, если игра приведена к матричной форме, рассмотрен у Е.С. Вентцель "Исследование операций".



