По мотивам теоремы Кантора-Бернштейна

[Dedekind]

Теорема: Пусть даны два множества $A$ и $B$ и пусть существуют инъекции $f: X\to Y$ и $g: Y\to X$. Тогда существует и биекция $h: X\to Y$.

Доказательство теоремы начинается с индуктивного определения таких множеств: $A_1 = X\setminus g(Y)$ и $A_{n+1}=g(f(A_n))$, затем идет доказательство как, например, тут.

Есть побочное утверждение, которое для доказательства не важно. Нужно доказать, что множества $A_n$ попарно не пересекаются. Доказать можно так: очевидно, что $A_1$ не пересекается с любым следующих $A_n$. Затем, если пересечение $A_n$ и $A_m$ непусто, то непусто и пересечение $A_{n-1}$ и $A_{m-1}$ (поскольку, если $x\in A_n\cap A_m$, то $f^{-1}g^{-1}(x)\in A_{n-1}\cap A_{m-1}$). Повторяя процесс, дойдем до противоречия, что пересечение $A_1$ с каким-то другим множеством из серии непусто.

Я не уверен, по поводу последнего утверждения. Это похоже на теорему об индукции, но в обратную сторону. Есть ли у нее какое-то строгое доказательство?

[dgwuqtj]

Это обычная индукция по $n$ для утверждения $\forall n \enskip \forall m > n \enskip A_n \cap A_m = \varnothing$.

[Dedekind]

dgwuqtj
Да, действительно, что-то я протупил, можно и обычной индукцией. Спасибо!

[skobar]

Dedekind

Можно нарисовать картинку из которой будет видно, что в точности происходит. В частности, справедливость утверждения будет наглядно видна.

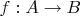
Во-первых, немного изменим обозначения. Будем обозначать наши множества $A$ и $B$ (вначале вы так и пишете, но потом почему-то меняете обозначения на $X$ и $Y$): $f: A\to B$ и $g: B\to A$ - инъекции. Вместо обозначения $A_n$ будем использовать $C_{n-1}$, как в ссылке на википедию:

$$C_0=A\setminus g(B),\quad C_{n+1}=g(f(C_n))$$

(обозначения $A_n$ у нас будут зарезервированы для других множеств)

Представим себе, что множества $A$ и $B$ с соответственными отображениями - это два зеркала друг напротив друга, и начнем процесс "отзеркаливания", то есть индукционно строим последовательность упорядоченных пар $(A_0,B_0), (A_1,B_1), (A_2, B_2), \dots$ следующим образом:

$$(A_0,B_0)\stackrel{\text{def}}{=}(A,B), \ \ (A_{k+1},B_{k+1})\stackrel{\text{def}}{=}(g(B_k), f(A_k))$$

Тривиально по индукции доказывается, что

$$f(A_k)\subset B_k\ \text{и}\ A_k \supset g(B_k)$$

поэтому

$$A=A_0 \supset A_1 \supset A_2 \supset \dots\ \text{и}\ B=B_0 \supset B_1 \supset B_2 \supset \dots$$

Поэтому имеем следующие разбиения множеств $A$ и $B$ на попарно непересекающиеся множества:

$$A=(A_0\setminus A_1)\cup (A_1\setminus A_2)\cup (A_2\setminus A_3)\cup\dots \cup (\cap_{i=0}^{\infty}A_i)$$ $$B=(B_0\setminus B_1)\cup (B_1\setminus B_2)\cup (B_2\setminus B_3)\cup\dots \cup (\cap_{i=0}^{\infty}B_i)$$

Для $k=0,1,2,\dots,\quad f$ будет биекцией из $A_k$ в $B_{k+1}$, а $g$ будет биекцией из $B_k$ в $A_{k+1}$. Тогда,

$$ f:A_k\setminus A_{k+1}\to B_{k+1}\setminus B_{k+2}\ \ \ \text{и}\ \ \ g:B_k\setminus B_{k+1}\to A_{k+1}\setminus A_{k+2} $$

также будут биекциями. Заметим также, что $f$ (как и $g^{-1}$) будет биекцией из $\cap_{i=0}^{\infty}A_i$ в $\cap_{i=0}^{\infty}B_i$. Таким образом у нас получается великолепная наглядная картинка, все стрелочки в которой являются биекциями между соответствующими прямоугольниками:

\begin{tikzpicture} \draw (0,0) rectangle (3,7); \draw (0,6)--(3,6); \draw [shift={(0,-1)}](0,6)--(3,6); \draw [shift={(0,-2)}](0,6)--(3,6); \draw [shift={(0,-3)}](0,6)--(3,6); \draw [shift={(0,-4.5)}](0,6)--(3,6); \node at (1.5,7.5) {$A$}; \draw (7,0) rectangle (10,7); \draw (7,6)--(10,6); \draw [shift={(0,-1)}](7,6)--(10,6); \draw [shift={(0,-2)}](7,6)--(10,6); \draw [shift={(0,-3)}](7,6)--(10,6); \draw [shift={(0,-4.5)}](7,6)--(10,6); \node at (8.5,7.5) {$B$}; \node at (1.5,6.5) {$A_0\setminus A_1$}; \node at (1.5,5.5) {$A_1\setminus A_2$}; \node at (1.5,4.5) {$A_2\setminus A_3$}; \node at (1.5,3.5) {$A_3\setminus A_4$}; \node at (1.5,2.25) {$\dots$}; \node at (1.5,0.75) {$\cap_{i=0}^{\infty}A_i$}; \node at (8.5,6.5) {$B_0\setminus B_1$}; \node at (8.5,5.5) {$B_1\setminus B_2$}; \node at (8.5,4.5) {$B_2\setminus B_3$}; \node at (8.5,3.5) {$B_3\setminus B_4$}; \node at (8.5,2.25) {$\dots$}; \node at (8.5,0.75) {$\cap_{i=0}^{\infty}B_i$}; \draw [->, thick, green] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); \draw [->, thick, green, shift={(0,-1)}] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); \draw [->, thick, green, shift={(0,-2)}] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); \draw [->, thick, green, shift={(0,-3)}] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); \draw [->, thick, green] (3.2,0.95)--(6.8,0.95); \draw [->, thick, red, shift={(10,0)}, xscale=-1] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); \draw [->, thick, red, shift={(10,-1)}, xscale=-1] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); \draw [->, thick, red, shift={(10,-2)}, xscale=-1] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); \draw [->, thick, red, shift={(10,-3)}, xscale=-1] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); \draw [<-, thick, red] (3.2,0.55)--(6.8,0.55); \node [green]at (4.5,6.7) {$f$}; \node [green]at (4.5,5.7) {$f$}; \node [green]at (4.5,4.7) {$f$}; \node [green]at (4.5,3.7) {$f$}; \node [green]at (4.9,1.3) {$f$}; \node [red]at (5.6,6.65) {$g$}; \node [red]at (5.6,5.65) {$g$}; \node [red]at (5.6,4.65) {$g$}; \node [red]at (5.6,3.65) {$g$}; \node [red]at (5.3,0.3) {$g$}; \end{tikzpicture}

С картинкой теперь все легко :) Последовательность множеств $C_0, C_1,\dots$, о которой шла речь - это $A_0\setminus A_1, A_2\setminus A_3,\dots$ ("прыгаем" по разбиению через одно множество) :

$$C_k=A_{2k}\setminus A_{2k+1}$$

Теперь попарная непересекаемость множеств $C_0, C_1,\dots$ вопросов не вызывает.

Также из картинки видно, как нужно переставить стрелочки, чтобы сконструировать биекцию из $A$ в $B$:
\begin{tikzpicture} \draw (0,0) rectangle (3,7); \draw (0,6)--(3,6); \draw [shift={(0,-1)}](0,6)--(3,6); \draw [shift={(0,-2)}](0,6)--(3,6); \draw [shift={(0,-3)}](0,6)--(3,6); \draw [shift={(0,-4.5)}](0,6)--(3,6); \node at (1.5,7.5) {$A$}; \draw (7,0) rectangle (10,7); \draw (7,6)--(10,6); \draw [shift={(0,-1)}](7,6)--(10,6); \draw [shift={(0,-2)}](7,6)--(10,6); \draw [shift={(0,-3)}](7,6)--(10,6); \draw [shift={(0,-4.5)}](7,6)--(10,6); \node at (8.5,7.5) {$B$}; \node at (1.5,6.5) {$A_0\setminus A_1$}; \node at (1.5,5.5) {$A_1\setminus A_2$}; \node at (1.5,4.5) {$A_2\setminus A_3$}; \node at (1.5,3.5) {$A_3\setminus A_4$}; \node at (1.5,2.25) {$\dots$}; \node at (1.5,0.75) {$\cap_{i=0}^{\infty}A_i$}; \node at (8.5,6.5) {$B_0\setminus B_1$}; \node at (8.5,5.5) {$B_1\setminus B_2$}; \node at (8.5,4.5) {$B_2\setminus B_3$}; \node at (8.5,3.5) {$B_3\setminus B_4$}; \node at (8.5,2.25) {$\dots$}; \node at (8.5,0.75) {$\cap_{i=0}^{\infty}B_i$}; \draw [->, thick, green] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); %\draw [->, thick, green, shift={(0,-1)}] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); \draw [->, thick, green, shift={(0,-2)}] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); %\draw [->, thick, green, shift={(0,-3)}] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); \draw [->, thick, green] (3.2,0.95)--(6.8,0.95); \draw [<-, thick, red, shift={(10,0)}, xscale=-1] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); %\draw [->, thick, red, shift={(10,-1)}, xscale=-1] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); \draw [<-, thick, red, shift={(10,-2)}, xscale=-1] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); %\draw [->, thick, red, shift={(10,-3)}, xscale=-1] (3.2,6.5).. controls (5,6.4) and (5.6,6.2).. (6.8,5.5); %\draw [<-, thick, red] (3.2,0.55)--(6.8,0.55); \node [green]at (4.5,6.7) {$f$}; \node [green]at (4.5,5.7) {$f$}; \node [green]at (4.5,4.7) {$f$}; \node [green]at (4.5,3.7) {$f$}; \node [green]at (4.9,1.3) {$f$}; \node [red]at (5.6,6.65) {$g^{-1}$}; %\node [red]at (5.6,5.65) {$g$}; \node [red]at (5.6,4.65) {$g^{-1}$}; %\node [red]at (5.6,3.65) {$g^$}; %\node [red]at (5.3,0.3) {$g$}; \node at (5,2.25) {$\dots$}; \end{tikzpicture}

[Dedekind]

skobar
Ого. Спасибо за подробный ответ:) Прошу прощения за неточность в обозначениях, просто задачу привел по учебнику, а ссылку дал на Вики, потому что она доступнее. Да, с картинками все понятно. Я тоже нарисовал, но немного по-другому, Ваш подход лучше. А Вы вручную рисовали в латехе?

[skobar]

Dedekind в сообщении #1678265 писал(а):

А Вы вручную рисовали в латехе?

Это пакет TIKZ - экспериментальным путем выяснил, что он установлен на движке форума. Код выглядит длинным, но на самом деле он проще, чем кажется - это просто многочисленный "copy-paste" с небольшими модификациями.