С помощью принципа максимума Понтрягина требуется решить вот такую задачку:

Решение:

Для

имеем три случая:

Для

Для

(с учетом граничных условий не подходит)
Для

Cлучай

:

Cлучай

Тут получается, что имеем бесконечное количество управляющих последовательностей

, переводящих

в
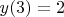
и дающих

Решение тут как бы очевидно с самого начала без привлечения принципа максимума (

). Но мне сперва показалось, что принцип максимума не отлавливает этих оптимальных ломанных решений с наклоном

. А потом я присмотрелся повнимательней и увидел, что

дает

Правильные ли это рассуждения и трактовка случая

?



