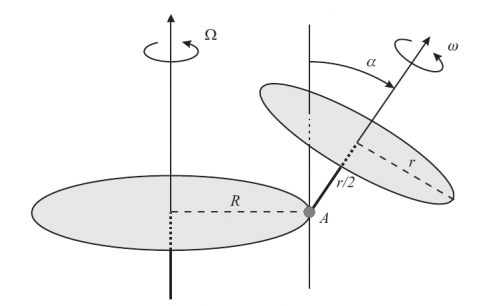
A top consists of of a homogeneous, circular disc of radius

,
and a light axis of length
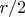
perpendicular to the disc through its center.
The axis is connected by a joint to a point
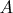
on the periphery of a horizontal
circular merry-go-round of radius
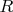
, so that the axis of the top can move
with negligible friction in a vertical plane containing the axis of the merry-
go-round. The merry-go-round has the constant angular velocity

about its
axis, and the top has the constant angular velocity
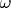
, relative to the merry-
go-round, about its axis. Find the angle
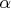
between the axis of the top and
the vertical.