Спасибо за ответы и советы, буду думать.
Еще возник вопрос по задаче из теорвера.
Есть база данных телефонных номеров, которая постоянно пополняется. Данным номерам периодически рассылаются сообщения. Возьмем номера для которых как минимум отправлялись 10 сообщений и посчитаем сколько было отправлено сообщений и сколько было из них доставлено и посчитаем так сказать

- коэффициент доставки сообщения на данный номер (назовем это приближенной вероятностью доставки сообщения):

Построим гистограмму по всем номерам в базе данных
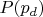
. И вот теперь я хочу решить простую задачу:
Найти вероятность того, что если для нового телефона в базе не было доставлено

сообщений подряд, то это телефон имеет

.
Я записал формулу Байеса:

Я хочу разобраться в формуле Байеса, могу ошибаться, но я посмотрел задачки и вот такую формулу написал исправьте, если не прав.
теперь запишем вероятность того, что было подряд

при вероятностях




И я вот запрограммировал данную формулу и когда устремляю

к большим числам то ожидаю стремление к 1, а получаю

Для проверки дам значения гистограммы

=[0.02 , 0.075, 0.125, 0.175, 0.225, 0.275, 0.325, 0.375, 0.425, 0.475, 0.525, 0.575, 0.625, 0.675, 0.725, 0.775, 0.825, 0.875, 0.925, 0.98 ]
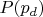
=[0.0598358 , 0.00579693, 0.01041777, 0.01367285, 0.01230709, 0.01669272, 0.01466683, 0.02500873, 0.01782327, 0.03230041, 0.01308861, 0.04002458, 0.0362839 , 0.05469141, 0.09438973, 0.08388091, 0.11350289, 0.17572879, 0.10465575, 0.07523104]
Подскажите, пожалуйста. что не так



