Круг разбит на 49 областей

[mavoumuro]

Круг разбит на 49 областей так, что никакие три области не
соприкасаются в одной точке. Полученная “карта” раскрашивается в три
цвета так, чтобы никакие две соседние области не имели одного цвета.
Граница двух областей считается окрашенной в оба цвета
Докажите, что найдутся две диаметрально противоположные точки, окрашенные
в один цвет.

[dgwuqtj]

Заведём функции $r, g, b$, которые показывают расстояния от точки до ближайшей точки, окрашенной в соответствующий цвет. Скажем, в красной области $r = 0$ и $b, g > 0$, а на границе красной и синей — $r = b = 0$ и $g > 0$. Эти функции непрерывны.

Теперь, если поделить каждую из этих функций на их сумму (которая всюду положительна), получится отображение из круга в границу треугольника в барицентрических координатах. Дальше топология.

[Rak so dna]

1. Заметим, что для того, что-бы разбить круг так, что-бы никакие три части не соприкасались в одной точке, необходимо, что-бы на границе этого круга находилось чётное количество двуцветных точек.

2. Предположим, что можно разбить окружность чётным числом двуцветных точек так, чтобы все диаметрально противоположные точки были разных цветов.

3. Рассмотрим окружность после разбиения. Она будет представлять из себя последовательность цветных дуг. Обозначим каждую из них первой буквой её цвета. Рассмотрим три последовательных дуги. Возможны два принципиальных случая (рис.1, рис.2), которые, для определенности, обозначим СКС и СКЗ.

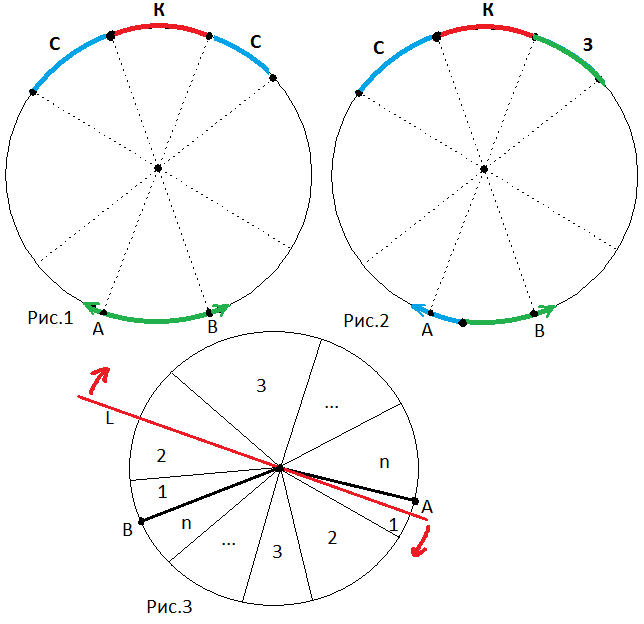
Рассмотрим дугу AB, которая лежит против дуки К.
3.1. В случае СКС точки А,В и их окрестности будут зелёного цвета, поэтому внутри дуги АВ лежит чётное число зелёно-синих точек. Поэтому, окрасив всю дугу АВ в зелёный цвет, мы не изменим ни чётность общего количества двуцветных точек на окружности, ни корректности разбиения окружности.
3.2. В случае СКЗ точка А и её окрестность будет синего цвета, точка В и её окрестность — зелёного. Поэтому, оставив внутри дуги АВ одну сине-зелёную точку, мы не изменим ни чётность общего количества двуцветных точек на окружности, ни корректности разбиения окружности.

4. Будем последовательно применять процедуру 3. ко всем подряд идущим трём дугам до тех пор, пока количество двуцветных точек на окружности не перестанет уменьшаться. В результате, мы получим корректно разбитую окружность, против каждой дуги которой, согласно 3.1. и 3.2., лежит либо одна, либо ноль двуцветных точек. Но количество двуцветных точек должно в точности равняться количеству дуг, а поэтому против кажной дуги лежит ровно одна двуцветная точка. А вся окружность может быть только вида СКЗСКЗ...СКЗ (с точностью до взаимной замены цветов).

5. Осталось показать, что при таком разбиении окружности, чётного количества дуг быть не может. Для этого достаточно показать (Рис.3), что прямая L, при повороте из А в В обязательно пройдёт через два сектора с одинаковыми номерами, а это очевидно. Т.о. пришли к противоречию с 2.

[dgwuqtj]

Rak so dna в сообщении #1673436 писал(а):

1. Заметим, что для того, что-бы разбить круг так, что-бы никакие три части не соприкасались в одной точке, необходимо, что-бы на границе этого круга находилось чётное количество двуцветных точек.

Это более-менее очевидно, если области ограничены жордановыми кривыми. А в общем случае почему этих точек вообще конечное число?

[Rak so dna]

dgwuqtj в сообщении #1673447 писал(а):

А в общем случае почему этих точек вообще конечное число?

Разделим все двуцветные точки на виды: КС, СК, КЗ, ЗК, СЗ, ЗС. Пусть, для определённости, на окружности бесконечное число красно-синих (КС) точек. Тогда хотя бы одна из $49$-й областей также должна содержать бесконечное количество таких КС точек. Отметим их на окружности. Поскольку все эти точки содержит одна область, их можно последовательно соединить непрерывными линиями, целиком лежащими в этой области. Каждая такая линия будет отсекать "кусок" круга, содержащий одновременно и красные и синие точки, а значит будет содержать в себе как минимум одну область целиком. А значит и общее число областей будет бесконечным.

[dgwuqtj]

У меня идея как-то попроще была, без необходимости строить кривые в области с концом в данной точке границы (кстати, где про это почитать?) и т.д. Просто если уже есть непрерывное отображение из диска в окружность, то его можно поднять до отображения в прямую (диск односвязен), и тогда по теореме Борсука — Улама пара противоположных точек границы диска отобразятся в одну точку. К тому же в одномерном случае теорема Борсука — Улама довольно очевидна.