Группы автоморфизмов групп диэдра

[B@R5uk]

Вот имеется группа диэдра:

$$\mathrm{D}_{2n}=\left\langle\;r,\;s\;|\;r^n=s^2=(rs)^2=I\;\right\rangle$$

Я пытаюсь понять (и, желательно, понятно доказать), как строить для неё группу автоморфизмов в случае произвольного n.

Утверждение, что порядок этой группы автоморфизмов

$$\left|\mathrm{Aut}\left(\mathrm{D}_{2n}\right)\right|=n\varphi(n)$$

встречается практически везде (я даже нашёл обсуждение того, когда автоморфизмы внутренние) и, если честно, довольно легко доказывается. Берём отображение, которое заменяет образующую r главного цикла группы на другую образующую этого цикла, а образующую s — любым другим элементом, не принадлежащим главному циклу (они все имеют порядок 2):

$$\begin{tabular}{lll}\sigma(r)=r^k,&1\,\le k\le n-1,&\gcd(n,\;k)=1\\ \sigma(s)=r^ls,&0\;\le l\le n-1\end{tabular}$$

Далее, пользуясь определением гомоморфизма продолжаем это отображение на все остальные элементы группы, убеждаемся, что все образы различны и, следовательно, покрывают всю группу, что означает построенный гомоморфизм на самом деле изоморфизм

$$\sigma\in\mathrm{Aut}\left(\mathrm{D}_{2n}\right)$$

Количество различных образов первой образующей определяется функцией Эйлера, количество различных образов второй равно n, а общее число способов — это произведение обеих величин. Однако, даже честно проделав вычисления, структура группы автоморфизмов из них просматриваться не будет.

Я попробовал забрутфорсить этот вопрос. Понасиловав мой слабенький компьютер моей глупой программой, получил результаты, в которых кое-что просматривается. Причём закономерности слишком регулярны, чтобы быть случайностью:

$$\begin{tabular}{l} \mathrm{Aut}\left(\mathrm{D}_4\right)\;\!\;=\mathrm{D}_6\\ \mathrm{Aut}\left(\mathrm{D}_8\right)\;\!\;=\mathrm{D}_8\\ \mathrm{Aut}\left(\mathrm{D}_{16}\right)=\mathbb{Z}_8\;\!\;\rtimes\left(\mathbb{Z}_2\times\mathbb{Z}_2\right)=\left\langle\;a,\;b,\;c\;|\;a^8\;\!\;=b^2=c^2=(ac)^2=I,\;a^b=a^3\;\right\rangle\\ \mathrm{Aut}\left(\mathrm{D}_{32}\right)=\mathbb{Z}_{16}\rtimes\left(\mathbb{Z}_4\times\mathbb{Z}_2\right)=\left\langle\;a,\;b,\;c\;|\;a^{16}=b^4=c^2=(ac)^2=I,\;a^b=a^3\;\right\rangle\\ \mathrm{Aut}\left(\mathrm{D}_{64}\right)=\mathbb{Z}_{32}\rtimes\left(\mathbb{Z}_8\times\mathbb{Z}_2\right)=\left\langle\;a,\;b,\;c\;|\;a^{32}=b^8=c^2=(ac)^2=I,\;a^b=a^3\;\right\rangle\\ \end{tabular}$$

$$\begin{tabular}{l} \mathrm{Aut}\left(\mathrm{D}_6\right)\;\!\;=\mathrm{D}_6\\ \mathrm{Aut}\left(\mathrm{D}_{12}\right)=\mathrm{Aut}\left(\mathrm{D}_6\right)\;\!\;\times\mathbb{Z}_2=\mathrm{D}_{12}\\ \mathrm{Aut}\left(\mathrm{D}_{20}\right)=\mathrm{Aut}\left(\mathrm{D}_{10}\right)\times\mathbb{Z}_2\\ \mathrm{Aut}\left(\mathrm{D}_{28}\right)=\mathrm{Aut}\left(\mathrm{D}_{14}\right)\times\mathbb{Z}_2\\ \mathrm{Aut}\left(\mathrm{D}_{36}\right)=\mathrm{Aut}\left(\mathrm{D}_{18}\right)\times\mathbb{Z}_2\\ \mathrm{Aut}\left(\mathrm{D}_{44}\right)=\mathrm{Aut}\left(\mathrm{D}_{22}\right)\times\mathbb{Z}_2\\ \mathrm{Aut}\left(\mathrm{D}_{52}\right)=\mathrm{Aut}\left(\mathrm{D}_{26}\right)\times\mathbb{Z}_2\\ \mathrm{Aut}\left(\mathrm{D}_{68}\right)=\mathrm{Aut}\left(\mathrm{D}_{34}\right)\times\mathbb{Z}_2\\ \mathrm{Aut}\left(\mathrm{D}_{76}\right)=\mathrm{Aut}\left(\mathrm{D}_{38}\right)\times\mathbb{Z}_2\\ \mathrm{Aut}\left(\mathrm{D}_{84}\right)=\mathrm{Aut}\left(\mathrm{D}_{42}\right)\times\mathbb{Z}_2\\ \mathrm{Aut}\left(\mathrm{D}_{92}\right)=\mathrm{Aut}\left(\mathrm{D}_{46}\right)\times\mathbb{Z}_2\\ \mathrm{Aut}\left(\mathrm{D}_{100}\right)=\mathrm{Aut}\left(\mathrm{D}_{50}\right)\times\mathbb{Z}_2\\ \end{tabular}$$

Первая очевидная закономерность: если m — нечётное, то

$$\mathrm{Aut}\left(\mathrm{D}_{4m}\right)=\mathrm{Aut}\left(\mathrm{D}_{2m}\right)\times\mathbb{Z}_2$$

при этом так же выполняется:

$$\mathrm{D}_{4m}=\mathrm{D}_{2m}\times\mathbb{Z}_2$$

Это не имеет отношение к автоморфизмам, просто ещё одно свойство групп диэдра. Далее эксперимент, где порядок главного цикла группы — это произвольное составное число. Результаты поразительно напоминают случай автоморфизмов обычных циклических групп:

$$\begin{tabular}{l} \mathrm{Aut}\left(\mathrm{D}_{24}\right)=\mathrm{Aut}\left(\mathrm{D}_8\;\!\;\right)\times\mathrm{Aut}\left(\mathrm{D}_6\right)\\ \mathrm{Aut}\left(\mathrm{D}_{30}\right)=\mathrm{Aut}\left(\mathrm{D}_{10}\right)\times\mathrm{Aut}\left(\mathrm{D}_6\right)\\ \mathrm{Aut}\left(\mathrm{D}_{40}\right)=\mathrm{Aut}\left(\mathrm{D}_{10}\right)\times\mathrm{Aut}\left(\mathrm{D}_8\right)\\ \mathrm{Aut}\left(\mathrm{D}_{42}\right)=\mathrm{Aut}\left(\mathrm{D}_{14}\right)\times\mathrm{Aut}\left(\mathrm{D}_6\right)\\ \mathrm{Aut}\left(\mathrm{D}_{48}\right)=\mathrm{Aut}\left(\mathrm{D}_{16}\right)\times\mathrm{Aut}\left(\mathrm{D}_6\right)\\ \mathrm{Aut}\left(\mathrm{D}_{56}\right)=\mathrm{Aut}\left(\mathrm{D}_{14}\right)\times\mathrm{Aut}\left(\mathrm{D}_8\right)\\ \mathrm{Aut}\left(\mathrm{D}_{60}\right)=\mathrm{Aut}\left(\mathrm{D}_{20}\right)\times\mathrm{Aut}\left(\mathrm{D}_6\right)\\ \mathrm{Aut}\left(\mathrm{D}_{66}\right)=\mathrm{Aut}\left(\mathrm{D}_{22}\right)\times\mathrm{Aut}\left(\mathrm{D}_6\right)\\ \mathrm{Aut}\left(\mathrm{D}_{70}\right)=\mathrm{Aut}\left(\mathrm{D}_{14}\right)\times\mathrm{Aut}\left(\mathrm{D}_{10}\right)\\ \mathrm{Aut}\left(\mathrm{D}_{72}\right)=\mathrm{Aut}\left(\mathrm{D}_{18}\right)\times\mathrm{Aut}\left(\mathrm{D}_8\right)\\ \mathrm{Aut}\left(\mathrm{D}_{78}\right)=\mathrm{Aut}\left(\mathrm{D}_{26}\right)\times\mathrm{Aut}\left(\mathrm{D}_6\right)\\ \mathrm{Aut}\left(\mathrm{D}_{80}\right)=\;?\\ \mathrm{Aut}\left(\mathrm{D}_{84}\right)=\mathrm{Aut}\left(\mathrm{D}_{26}\right)\times\mathrm{Aut}\left(\mathrm{D}_6\right)\\ \mathrm{Aut}\left(\mathrm{D}_{84}\right)=\mathrm{Aut}\left(\mathrm{D}_{14}\right)\times\mathrm{Aut}\left(\mathrm{D}_{12}\right)\\ \mathrm{Aut}\left(\mathrm{D}_{88}\right)=\mathrm{Aut}\left(\mathrm{D}_{22}\right)\times\mathrm{Aut}\left(\mathrm{D}_8\right)\\ \mathrm{Aut}\left(\mathrm{D}_{90}\right)=\mathrm{Aut}\left(\mathrm{D}_{18}\right)\times\mathrm{Aut}\left(\mathrm{D}_{10}\right)\\ \mathrm{Aut}\left(\mathrm{D}_{96}\right)=\;?\\ \mathrm{Aut}\left(\mathrm{D}_{102}\right)=\mathrm{Aut}\left(\mathrm{D}_{34}\right)\times\mathrm{Aut}\left(\mathrm{D}_6\right)\\ \mathrm{Aut}\left(\mathrm{D}_{104}\right)=\mathrm{Aut}\left(\mathrm{D}_{26}\right)\times\mathrm{Aut}\left(\mathrm{D}_8\right)\\ \end{tabular}$$

Здесь закономерность прослеживается такая: если m и n — нечётные числа, то

$$\mathrm{Aut}\left(\mathrm{D}_{2mn}\right)=\mathrm{Aut}\left(\mathrm{D}_{2m}\right)\times\mathrm{Aut}\left(\mathrm{D}_{2n}\right)$$

Что происходит в случае, когда порядок главного цикла является произведением степени двойки на нечётное, я по двум опорным точкам судить не возьмусь (моя программка автоморфизмы для 80 и 96 за разумное время не осилила). Ну, может кроме вот этой закономерности:

$$\mathrm{Aut}\left(\mathrm{D}_{8m}\right)=\mathrm{Aut}\left(\mathrm{D}_{2m}\right)\times\mathrm{D}_8$$

И, наконец, случай, когда порядок главного цикла группы диэдра является нечётным простым числом или степенью такового. Я даже не буду выписывать примеры, сразу приведу предполагаемую общую формулу:

$$\mathrm{Aut}\left(\mathrm{D}_{2n}\right)=\mathbb{Z}_n\overset{k}{\rtimes}\mathbb{Z}_{\varphi(n)}=\left\langle\;a,\;b\;\left|\;a^n=b^{\varphi(n)}=I,\;a^b=a^k\;\right.\right\rangle$$

Общий вид обменной степени k угадать не получается. Это осложняется ещё тем, что для неё обычно целая куча допустимых значений (дающих одну и ту же группу). По этой причине я составил табличку:

Используется синтаксис Text

n       k
3       2
5       2, 3
7       3, 5
11      2, 6, 7, 8
13      2, 6, 7, 11
17      3, 5, 6, 7, 10, 11, 12, 14
19      2, 3, 10, 13, 14, 15
23      5, 7, 10, 11, 14, 15, 17, 19, 20, 21
29      2, 3, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27
31      3, 11, 12, 13, 17, 21, 22, 24
37      2, 5, 13, 15, 17, 18, 19, 20, 22, 24, 32, 35
41      6, 7, 11, 12, 13, 15, 17, 19, 22, 24, 26, 28, 29, 30, 34, 35
43      3, 5, 12, 18, 19, 20, 26, 28, 29, 30, 33, 34
47      5, 10, 11, 13, 15, 19, 20, 22, 23, 26, 29, 30, 31, 33, 35, 38, 39, 40, 41, 43, 44, 45

9       2, 5
25      2, 3, 8, 12, 13, 17, 22, 23
27      2, 5, 11, 14, 20, 23
49      3, 5, 10, 12, 17, 24, 26, 33, 38, 40, 45, 47

 

Интересно, на сколько сложная нужна теория, чтобы гипотезы выше доказать (или опровергнуть)? Кто-нибудь, где-нибудь уже проделывал это? Что-то мне поиск ничего толкового не даёт.

[schmetterling]

Ответ простой, но нет желания сразу его раскрывать.

Вы предполагаете, что получится какое-то полупрямое произведение. Причём была здравая мысль задавать автоморфизм на образующих. А теперь попробуйте найти две подгруппы попроще в $\operatorname{Aut}(D_{2n})$, и доказать, что они образуют полупрямое произведение, и в терминах этих подгрупп описать $k$ — вот вам и структура.

[dgwuqtj]

Есть такая чудесная группа аффинных преобразований прямой $\mathrm{Aff}(1, R)$ над коммутативным кольцом $R$ с единицей. Она состоит из всех многочленов первой степени $a x + b$ с обратимым старшим коэффициентом $a$, групповая операция — композиция. Можете проверить, что ваша диэдральная группа вкладывается в $\mathrm{Aff}(1, \mathbb Z / 2 n \mathbb Z)$ как нормальная подгруппа с образующими $-x$ и $x + 2$. Утверждается, что при $n \geq 3$ все автоморфизмы получаются из действия этой большей группы сопряжением. Те многочлены, которые перестановочны с диэдральной группой, (т.н. 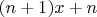централизатор) — это $x$, $x + n$, а ещё $(n + 1) x$ и $(n + 1) x + n$ при чётном $n$. Удивительным образом это как раз ядро сюръективного гомоморфизма $\mathrm{Aff}(1, \mathbb Z / 2 n \mathbb Z) \to \mathrm{Aff}(1, \mathbb Z / n \mathbb Z)$, то есть те многочлены, которые сравнимы с $x$ по модулю $n$. Поэтому группа автоморфизмов изоморфна $\mathrm{Aff}(1, \mathbb Z / n \mathbb Z)$ в любом случае. Ну и при $n \leq 2$ будет исключение.

Как группа, разумеется, $\mathrm{Aff}(1, R) \cong R \rtimes R^*$. Поэтому ваша предполагаемая формула для $D_{2 n}$ вряд ли верна.

[B@R5uk]

schmetterling в сообщении #1671691 писал(а):

А теперь попробуйте найти две подгруппы попроще в $\operatorname{Aut}(D_{2n})$, и доказать, что они образуют полупрямое произведение

Не совсем понял, что вы имеете в виду. Вот, например, автоморфизм группы и его нормальный ряд подгрупп:

$$\mathrm{Aut}\left(\mathrm{D}_{34}\right)=\left[\mathbb{Z}_{17}\overset{3}{\rtimes}\mathbb{Z}_{16}\right]\triangleleft\left[\mathbb{Z}_{17}\overset{2}{\rtimes}\mathbb{Z}_{8}\right]\triangleleft\left[\mathbb{Z}_{17}\overset{4}{\rtimes}\mathbb{Z}_{4}\right]\triangleleft\mathrm{D}_{34}\triangleleft\mathbb{Z}_{17}$$

можете на нём пояснить, что вы имели в виду? Это единственные подгруппы, которые не являются циклами, к тому же они характеристические (присутствуют в единственном экземпляре).

dgwuqtj в сообщении #1671694 писал(а):

вряд ли верна

Она работает для n из таблички по крайней мере, дальше не проверял. На каком приблизительно n можно ожидать контр-пример?

dgwuqtj в сообщении #1671694 писал(а):

диэдральная группа вкладывается в $\mathrm{Aff}(1, \mathbb Z / 2 n \mathbb Z)$ как нормальная подгруппа

Вроде же обсуждали в соседней теме, что вложение может привести к потере автоморфизмов. Или я что-то не допонял?

[dgwuqtj]

B@R5uk в сообщении #1671710 писал(а):

Или я что-то не допонял?

Это особенное вложение. Можно же посчитать, что $\mathrm{Aff}(1, \mathbb Z / 2 n \mathbb Z)$ задаёт ровно $n \cdot \varphi(n)$ автоморфизмов, а вы уже знаете, что их ровно столько.

B@R5uk в сообщении #1671710 писал(а):

На каком приблизительно n можно ожидать контр-пример?

Ааа, я не так прочитал. У вас все закономерности правильные, не будет там контрпримеров.

[schmetterling]

B@R5uk
Под "найти" я имел в виду задать действием на образующих. Вот вы автоморфизмы задаёте образами образующих $r \mapsto r^k$, $s \mapsto r^l s$. И можно накладывать какие-то ограничения на $k, l$, а если эти ограничения достаточно хорошие — подмножество автоморфизмов, которое ими задаётся, будет подгруппой. Я предлагаю таким способом описать две совсем-совсем простые (но нетривиальные) подгруппы, и показать, что на них можно смотреть как на полупрямые сомножители.

-- 28.01.2025, 06:03 --

И да, никаких проблем, если эти подгруппы будут циклами — тем проще структура группы.