Теорема о дифференцируемости сложной функции

[curly_bracket]

Здравствуйте.

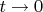
Смотрел 22 лекцию Станислава Валерьевича Шапошникова по математическому анализу и застрял на доказательстве теоремы о дифференцируемости сложной функции, так как не понимаю момент на 1:29:36 (не понимаю вообще всю идею с доопределением бесконечно малой при $t \to 0$ функции $\beta(t)$ в нуле).

Вот теорема о дифференцируемости сложной функции в формулировке С. В.:
Пусть функция $f : U(a) \to V(f(a))$, $g : V(f(a)) \to \mathbb{R}$, $f$ дифференцируема в точке $a$ и $g$ дифференцируема в точке $f(a)$. Тогда $g(f(x))$ дифференцируема в точке $a$, причем

$$(g(f(x))'(a) = g'(f(a))f'(a)).$$

Доказательство. Так как $f$ дифференцируема в точке $a$, то $f(a+h) - f(a) = f'(a)h + \alpha(h)h$, где $\displaystyle \lim_{h \to 0} \alpha(h) = 0$.
Так как $g$ дифференцируема в точке $a$, то $g(f(a)+t) - g(f(a)) = g'(f(a))t + \beta(t)t$, где $\displaystyle \lim_{t \to 0} \beta(t) = 0$.
Доопределим $\beta(0) = 0$. Тогда предыдущее равенство принимает вид

$$g(f(a+h)) - g(f(a)) = g'(f(a))(f(a+h)-f(a)) + \beta(f(a+h) - f(a))(f(a+h)-f(a)),$$

правая часть которого представляется в виде

$$g'(f(a))f'(a)h + (g'(f(a))\alpha(h) + \beta(f(a+h) - f(a))(f'(a) + \alpha(h)))h.$$

Здесь С. В. делает акцент на то, что после доопределения $\beta(0)=0$ появился ранее несуществующий предел $\displaystyle \lim_{h \to 0} \beta(f(a+h) - f(a)) = 0$, так как $\beta$ стала композицией непрерывных функций.
Он не проговорил конец доказательства, я понял так: записываем предел отношения полученного приращения сложной функции $g(f(x))$ и $h$ при $h\to 0$ и получаем $g'(f(a))f'(a)$, т.е.

$$\lim_{h \to 0} \frac{g'(f(a))f'(a)h + (g'(f(a))\alpha(h) + \beta(f(a+h) - f(a))(f'(a) + \alpha(h)))h}{h} = g'(f(a))f'(a).$$

Как я понял объяснение С. В. о маневре с доопределением функции $\beta$ в нуле: нам нужно доопределить $\beta$ в нуле, чтобы равенство $t = f(a + h) - f(a)$, являющееся приращением аргумента функции $\beta$, было верно и в случае $h = 0$. Случай $h = 0$ возможен, так как $f(x)$ непрерывна в точке $a$, т.е. существует предел $\displaystyle \lim_{h \to 0} (f(h + a) - f(a)) = 0$. Также необходимым для существования предела $\displaystyle \lim_{h \to 0} \beta(f(a+h) - f(a)) = 0$ является факт, что теперь $\beta$ --- композиция двух непрерывных функций.

Далее мое мнение.
Существование случая $h = 0$ не мешает нашей сложной функции $g(f(x))$ иметь предел при $h\to 0$, т.к. $h=0$ --- предельная точка, значение функции в которой не имеет значения, важен именно предел этой функции. Также не важен тот факт, что $\beta$ стала композицией двух непрерывных функций после доопределения, так как внутренней и внешней функциям необязательно быть непрерывными, чтобы их сложная функция имела предел. В подтверждение (как мне кажется) своих слов привожу теорему о пределе сложной функции в формулировке самого С.В. (из лекции 14, 1:10:36):
Пусть $D \subset \mathbb{R}$ и $E \subset \mathbb{R}$, пусть $f : D \to E$ и $E \to \mathbb{R}$ и пусть $a$ --- предельная точка $D$, $b$ --- предельная точка $E$. Предположим, что

$$\lim_{x \to a} f(x) = b \text{ и } \lim_{y \to b} g(y) = c,$$

и существует проколотая окрестность $U'(a)$ такая, что $\forall x \in U'(a) \cap D$ выполнено $f(x)\neq b$. Тогда

$$\lim_{x \to a} g(f(x)) = c.$$

Конец формулировки теоремы.

В формулировке этой теоремы я не вижу слов о том, что внутренняя и/или сложная функции должны быть непрерывны в предельной точке $a$, или о том, что внешняя функция должна быть непрерывна в предельной точке $b$. Предел $\displaystyle \lim_{h \to 0} \beta(f(a+h) - f(a)) = 0$ так и так будет существовать, потому что $\beta \to 0$, когда $f(a + h) - f(a) \to 0$, а $f(a+h) - f(a) \to 0$, когда $h\to 0$.

Изложенные мысли заставляют меня думать, что доопределение функции $\beta$ не играет никакой роли в доказательстве. Почему я неправ?

[Combat Zone]

curly_bracket в сообщении #1668386 писал(а):

Изложенные мысли заставляют меня думать, что доопределение функции $\beta$ не играет никакой роли в доказательстве. Почему я неправ?

Потому что никто не обещал вам, что в проколотой окрестности точки $a$ функция $f$ не будет обращаться в $f(a)$. Второе условие процитированной вами теоремы о пределе композиции не работает, поэтому используется другая ее часть (или другая теорема), - не буду уж смотреть как там рассказывал именно этот лектор. Для другой теоремы о пределе композиции, когда условие

curly_bracket в сообщении #1668386 писал(а):

существует проколотая окрестность $U'(a)$ такая, что $\forall x \in U'(a) \cap D$ выполнено $f(x)\neq b$

потенциально может нарушаться, требуется непрерывность в нужной точке функции $g$, в тексте основной теоремы ее роль играет $\beta$.

[Combat Zone]

curly_bracket в сообщении #1668386 писал(а):

не понимаю вообще всю идею с доопределением бесконечно малой при $t \to 0$ функции $\beta(t)$ в нуле

Добавлю все-таки.
Основная причина непонимания этого места обычно в том, что человек не вполне понимает, что такое $\lim_{t\to 0} \beta (t) =0$.
Здесь принципиально важно, что $t$ стремится к нулю, в ноль не попадая - т.е. бегает по проколотой окрестности нуля.
Вам же, по ходу доказательства, нужно уметь вместо $t$ подставить $t=f(a+h)-f(a), \ h\to 0$. Оно конечно, $h$ тоже бегает по проколотой окрестности нуля, но при сколь угодно малых $h$ даже из проколотой окрестности, само выражение в правой части может сколь угодно много раз обращаться в ноль. (Например, для функции $f(x)= x^2\sin 1/x, \ a=0$.) Тогда такое $t$ не из проколотой окрестности нуля, так что механически записать $\beta (f(a+h)-f(a)) \to 0, \ h\to 0$ нельзя - аргумент у бета нельзя изолировать от нуля, он туда слишком часто попадает. Так что это и не делается. Делается иначе, как - вы видели.

[curly_bracket]

Combat Zone
Спасибо! Как раз последние три часа перечитывал ваш первый ответ, додумываясь до того, что вы объяснили вторым :). Необходимость доопределения $\beta$ в нуле в контексте нашего доказательства я понял.

"Другой части/теоремы о пределе композиции" я не нахожу ни в Зориче, ни в Кудрявцеве, ни в Морозовой. Она, наверное, формулируется следующим образом?
Пусть $y = f(x)$ определена в $U(a)$ и непрерывна в $a$, $g(y)$ определена в $U(f(a))$ и непрерывна в $f(a)$, и в $U(a)$ определена сложная функция $g(f(x))$. Тогда существует предел

$$\lim_{x \to a} g(f(x)) = g(f(a)).$$

Кажется, ее доказательство совсем простое: по теореме о непрерывности композиции непрерывных функций, $g(f(x))$ непрерывна в точке $a$. Из определения непрерывности следует, что $\displaystyle \lim_{x \to a} g(f(x)) = g(f(a))$. Может, поэтому она отдельно в учебниках и не упоминается (или я неправильно формулирую/доказываю/читаю).

[Combat Zone]

Да, здесь можно и этот результат использовать. Поскольку $f$ непрерывна в точке $a$.

-- 04.01.2025, 13:12 --

Теорема о пределе композиции (2) выглядит так:

Пусть $D \subset \mathbb{R}$ и $E \subset \mathbb{R}$, пусть $f : D \to E$ и $E \to \mathbb{R}$ и пусть $a$ --- предельная точка $D$, $b$ --- предельная точка $E$. Предположим, что

$$\lim_{x \to a} f(x) = b \text{ и } \lim_{y \to b} g(y) = g(b),$$

то есть $g$ непрерывна в точке $b$.
Тогда

$$\lim_{x \to a} g(f(x)) = g(b).$$

Разница с теоремой о композиции непрерывных очевидна - непрерывность $f$ не требуется. Так что это более общий случай. Доказывается она тоже легко, можете попробовать сами, интереса ради. Но вам, действительно, хватит и композиции непрерывных.