A circle is inscribed in triangle

. Let

be the point of contact of the circle and the side

and

be the point on the circle, diametrical to the point

. We draw the line
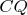
which intersects the side

at the point

. Prove that the midpoint of the length

is also the midpoint of the length

.