Чтобы вертикальные отрезки вписать в схему кусочно-гладких экстремалей, надо задачу рассматривать в параметрической форме. Далее, задача допускает только односторонние вариации -- мы не можем сделать функцийю

отрицательной, а функцию

в параметрической форме -- убывающей. Поэтому эти куски кривой не обязаны быть экстремалями (вариация объема на них должна быть отрицательной при вариациях, сохраняющих площадь поверхности).
Я в условии добавил различные варианты значений площади поверхности.
Думаю, что ответ такой: при

искомая кривая -- окружность с центром на оси

, проходящая через точку

(соответствующий сосуд имеет форму сферического сегмента); при

у сосуда появляется доннышко, радиус которого растет с увеличением

, сама кривая становится той самой
Nodary, причём

, а

, причём

и убывает при возрастаниии

; при дальнейшем увеличении

производная

становится бесконечной, далее к кривой добавляется вертикальный отрезок (вокруг горлышка сосуда начинает расти плоское кольцо). Далее при возрастании

характер профиля не меняется (вертикальный отрезок, Nodary, касающаяся прямых

и
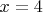
, вертикальный отрезок).