Задачка от
Padawan:
Доказать что множество действительных чисел нельзя представить в виде счетного семейства замкнутых не пересекающихся множеств.
ChatGPT:
Цитата:
Чтобы доказать, что множество действительных чисел

нельзя представить в виде счетного семейства замкнутых непересекающихся множеств, воспользуемся методом от противного.
Предположим, что существует счетное семейство замкнутых непересекающихся множеств

, такое что:

где

для

.
Поскольку каждое

является замкнутым множеством в

, оно является и ограниченным, или неограниченным.
Если хотя бы одно из множеств  неограниченно, то оно будет содержать все числа, превышающие некоторую величину,
неограниченно, то оно будет содержать все числа, превышающие некоторую величину, и, следовательно, не может быть непересекающимся с другими множествами, если они тоже неограниченные.
Теперь рассмотрим случай, когда все множества

ограничены. Поскольку каждое

замкнуто и ограничено, оно является компактным по теореме Больцано-Вейрштраса. Это означает, что каждое

содержит свои предельные точки и является замкнутым.
Счетное объединение компактных множеств может быть не компактным, но в случае,
если все  непересекающиеся и ограниченные, их объединение также будет ограниченным.
непересекающиеся и ограниченные, их объединение также будет ограниченным. Однако, учитывая, что

не является ограниченным множеством, мы получаем противоречие.
Кроме того, если бы

можно было выразить как счетное объединение непересекающихся замкнутых множеств, то из этого следовало бы, что

можно было бы перечислить, что противоречит свойству континуума (размерности) действительных чисел, согласно теореме Кантора о континууме.
Таким образом, мы приходим к выводу, что наше предположение неверно. Следовательно, множество действительных чисел нельзя представить в виде счетного семейства замкнутых непересекающихся множеств.
Ошибка сразу. Подчеркивание мое.
-- 09.11.2024, 15:21 --Дальше смешнее
я:
Цитата:
Доказать что множество действительных чисел можно представить в виде счетного семейства замкнутых непересекающихся множеств.
ChatGPT:
Цитата:
Чтобы доказать, что множество действительных чисел

можно представить в виде счетного семейства замкнутых непересекающихся множеств, мы можем использовать следующий подход:
1. **Определение множеств**: Рассмотрим множество

и разделим его на интервале
![$[-n, n]$ $[-n, n]$](https://dxdy-04.korotkov.co.uk/f/7/d/4/7d41e144765e1356ab9ac956bd8bc16f82.png)
для каждого натурального числа

. Мы можем представить

как объединение следующих замкнутых множеств:
![$$
A_n = [-n, n]
$$ $$
A_n = [-n, n]
$$](https://dxdy-02.korotkov.co.uk/f/9/5/4/954a07b24309d2ff0ac5e61c3811cd6482.png)
для

.
2. **Добавление множеств для положительных и отрицательных чисел**: Мы можем дополнительно разделить каждое

на два непересекающихся подмножества:
![$$
B_n = [-n, -n + 1] \quad \text{и} \quad C_n = [n - 1, n]
$$ $$
B_n = [-n, -n + 1] \quad \text{и} \quad C_n = [n - 1, n]
$$](https://dxdy-01.korotkov.co.uk/f/0/d/7/0d75806696a4e496f516b535c80bc67a82.png)
Таким образом, мы можем определить следующее множество:

3. **Непересекаемость**: Множества

для разных

будут непересекающимися:

Это происходит потому, что, например,
![$A_1 = [-1, 1]$ $A_1 = [-1, 1]$](https://dxdy-01.korotkov.co.uk/f/c/6/1/c616966ac5842c752b9ae72ac1d75fa282.png)
и
![$A_2 = [-2, 2]$ $A_2 = [-2, 2]$](https://dxdy-04.korotkov.co.uk/f/7/1/c/71c384f50c050a472c26227cc5bbd54782.png)
не пересекаются, и так далее для других значений

.
4. **Объединение**: Теперь мы можем записать:

Это объединение охватывает все действительные числа, так как для любого

существует такое

, что

.
Таким образом, мы можем представить множество действительных чисел

как счетное объединение замкнутых непересекающихся множеств

.
Следовательно, множество действительных чисел можно представить в виде счетного семейства замкнутых непересекающихся множеств.
До кучи:
Вещественная функция вещественной переменной непрерывна на замкнутом отрезке, дифференцируема во всех его внутренних точках и равна нулю на концах этого отрезка. Доказать, что внутри отрезка не существует точки, в которой значения функции и её первой производной совпадут.
Chat:
Цитата:
Рассмотрим непрерывную функцию

на замкнутом отрезке
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
, которая дифференцируема во всех внутренних точках и удовлетворяет условиям:
1.

2.

Мы хотим доказать, что внутри отрезка

не существует точки

, такой что

.
Предположим, что существует такая точка

, что

.
Рассмотрим функцию

для
![$ x \in [a, b] $ $ x \in [a, b] $](https://dxdy-02.korotkov.co.uk/f/9/1/5/9153d3c5ce8766f6d76df0acd94ce23982.png)
. Функция

будет непрерывной, так как

и

непрерывны (последняя из-за дифференцируемости).
Теперь оценим
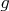
на концах отрезка:
- На

:

- На

:

Оба значения

и

равны нулю, так как

и

.
Теперь, так как

(по предположению), мы имеем, что

.
По теореме о промежуточных значениях, если

и

имеют одинаковый знак, а

, то
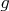
должно иметь хотя бы одну точку максимума или минимума на интервале

.
Поскольку

, и по теореме Ферма, если
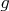
имеет максимум или минимум в точке

, то

, что приводит к равенству:

что не может быть, если

.
Таким образом, мы приходим к противоречию, что означает, что наше предположение о существовании такой точки

было неверным.
Следовательно, внутри отрезка

не существует точки, в которой значения функции

и её первой производной

совпадают.