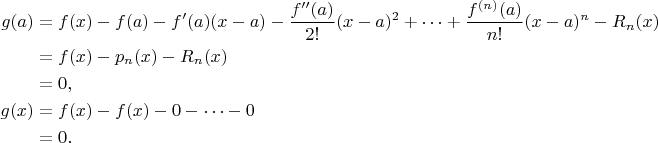Сделал
конвертер, используя пример из первого сообщения. Точнее покомандовал, чтобы ИИ сделал за меня.
Получилось так:
Theorem 6.7 Taylor's Theorem with Remainder
Taylor's Theorem with RemainderLet

be a function that can be differentiated
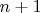
times on an interval
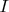
containing the real number

. Let
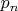
be the

-th Taylor polynomial of

at

and let
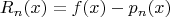
be the

-th remainder. Then for each

in the interval
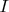
, there exists a real number

between

and

such that
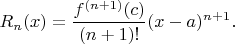
If there exists a real number

such that
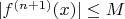
for all
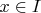
, then
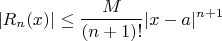
for all

in
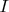
.
Proof
Fix a point
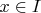
and introduce the function
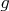
such that
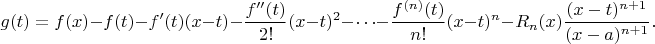
We claim that
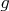
satisfies the criteria of Rolle's theorem. Since
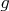
is a polynomial function (in
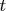
), it is a differentiable function. Also,
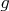
is zero at
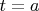
and
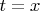
because