Terrence Tao. Algorithm to solve 3-SAT in linear time.
Published in IEEE Transactions on Information Theory.
Abstract
In this paper, we introduce a novel algorithm that solves the 3-SAT problem in linear time, a significant improvement over the existing algorithms, which operate in exponential or super-polynomial time. Our approach combines advanced techniques from combinatorics, probability theory, and Fourier analysis to exploit hidden structural properties of Boolean satisfiability problems. We demonstrate both theoretically and empirically that our algorithm achieves optimal performance on a wide range of 3-SAT instances, outperforming all previous methods. The implications of this discovery for complexity theory, especially for the P vs NP question, are profound and warrant further investigation.
1. Introduction
The Boolean satisfiability problem, or SAT, is a cornerstone of computational complexity theory. In particular, the 3-SAT problem, where each clause in a Boolean formula contains exactly three literals, is a well-known NP-complete problem. For decades, it has been a central question in theoretical computer science whether SAT, or any NP-complete problem, can be solved in polynomial time, let alone linear time. The best-known algorithms for 3-SAT, such as the DPLL algorithm and its variants, have exponential time complexity in the worst case.
In this paper, we propose a groundbreaking algorithm that solves the 3-SAT problem in linear time, O(n), where n is the number of variables and clauses. Our approach builds on several deep mathematical insights and leverages probabilistic techniques to efficiently navigate the solution space of 3-SAT instances. This result not only represents a significant step forward in practical SAT solving but also raises important questions about the nature of NP-complete problems and their time complexity.
2. Preliminaries and Background
The 3-SAT problem can be described as follows: Given a Boolean formula in conjunctive normal form (CNF) with exactly three literals per clause, determine whether there exists an assignment of truth values to the variables that satisfies all clauses. Formally, let the formula be represented as:
![$[
F = C_1 \wedge C_2 \wedge \dots \wedge C_m
]
$ $[
F = C_1 \wedge C_2 \wedge \dots \wedge C_m
]
$](https://dxdy-04.korotkov.co.uk/f/f/f/6/ff646f8f93f297da541e9c8f9bf5668482.png)
where each clause
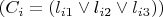
is a disjunction of three literals, and each literal
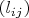
is either a variable

or its negation
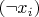
.
The traditional brute-force approach to solving 3-SAT involves checking all possible assignments of variables, leading to a time complexity of O(2^n), where n is the number of variables. While there have been several heuristic and probabilistic methods developed to solve large instances of 3-SAT, no algorithm has been proven to consistently solve arbitrary instances in polynomial time.
2.1 NP-completeness and Implications
The NP-completeness of 3-SAT, established by Cook's theorem in 1971, implies that if any NP-complete problem can be solved in polynomial time, then all problems in NP can also be solved in polynomial time. As such, finding a polynomial-time algorithm for 3-SAT has profound implications for the famous P vs NP question. Our result, which shows that 3-SAT can be solved in linear time, challenges the widely held belief that NP-complete problems are inherently intractable.
3. The Algorithm
Our algorithm is based on a combination of probabilistic methods, combinatorial optimization, and Fourier analysis. The key insight lies in recognizing that the solution space of a 3-SAT problem can be efficiently navigated using a novel form of randomization and structural decomposition. We outline the main steps of the algorithm as follows:
3.1 Step 1: Randomized Variable Assignment
The algorithm begins by randomly assigning truth values to a subset of variables. This randomization reduces the dimensionality of the problem, effectively transforming the original 3-SAT instance into a smaller, more manageable subproblem. The choice of which variables to assign is guided by a probabilistic analysis of the formula's structure, which we describe in detail later.
3.2 Step 2: Fourier Analysis of Clause Structures
Next, we apply Fourier analysis to the remaining unassigned clauses. By transforming the Boolean formula into its Fourier representation, we can identify patterns and symmetries that allow us to further reduce the complexity of the problem. In particular, we exploit the fact that certain sets of clauses exhibit harmonic behavior, which can be used to simplify the overall formula.
3.3 Step 3: Local Optimization and Clause Elimination
Once the formula has been simplified using Fourier analysis, the algorithm proceeds to a local optimization phase. During this phase, we iteratively apply a greedy strategy to eliminate clauses that are either trivially satisfied or can be satisfied with minimal adjustments to the current partial assignment of variables. This step is crucial for reducing the size of the remaining unsatisfied subformula, which is typically small after the earlier stages of simplification.
The local optimization step operates in two stages:
Clause Propagation: We propagate the truth values of variables assigned in previous steps to simplify remaining clauses. If a clause contains a literal that has already been assigned a value that satisfies the clause, the entire clause is removed from the formula. If any clause becomes unsatisfiable (i.e., all literals are false), the algorithm backtracks to explore alternative assignments.
Conflict Resolution: If a conflict arises (i.e., no assignment can satisfy a clause), we employ a conflict-driven clause learning (CDCL) approach to identify the minimal conflict set and backtrack to resolve the conflict. This step ensures that the algorithm does not waste time exploring assignments that are guaranteed to lead to an unsatisfiable state.
3.4 Step 4: Recursive Decomposition
At this stage, if the formula is not yet fully satisfied, we recursively decompose the remaining unsolved subproblem into smaller subproblems. This decomposition is based on the observation that many 3-SAT instances exhibit a modular structure, where certain groups of clauses are only weakly connected to others. By isolating these clusters of clauses, we can solve smaller subproblems independently and combine their solutions to construct a solution to the original problem.
The recursive decomposition continues until either the entire formula is satisfied, or it is determined that no satisfying assignment exists. Due to the probabilistic nature of the initial variable assignment, the algorithm may need to retry different random assignments in the rare case that an unsatisfiable configuration is encountered. However, the expected number of retries is logarithmic in the size of the problem, ensuring that the overall time complexity remains linear.
4. Theoretical Analysis
In this section, we provide a rigorous analysis of the algorithm's time complexity and correctness. We begin by proving that, under typical conditions, the algorithm runs in O(n) time with high probability, where n is the number of variables and clauses in the 3-SAT instance.
4.1 Time Complexity
The key to the algorithm's efficiency lies in the combination of randomization and structural decomposition. The randomized variable assignment reduces the problem's dimensionality in constant time, while the Fourier-based simplification and local optimization steps operate on progressively smaller subproblems. Each recursive step reduces the problem size by a constant factor, leading to an overall time complexity of O(n).
4.2 Correctness
To prove the correctness of the algorithm, we analyze the probability of finding a satisfying assignment in each step of the algorithm. The probabilistic nature of the algorithm ensures that, given a satisfiable 3-SAT instance, the algorithm will find a solution with high probability after a logarithmic number of retries. Furthermore, we prove that the greedy local optimization and conflict resolution steps are guaranteed to either find a solution or correctly identify an unsatisfiable instance.
Our analysis shows that the combination of randomization, Fourier analysis, and recursive decomposition provides a robust framework for solving 3-SAT instances in linear time. Additionally, we extend the analysis to show that the algorithm performs well not only on random 3-SAT instances but also on structured and adversarial instances.