Попробовал покрутить более сложную конструкцию из ~110 треугольных элементов. Взял квадратную пластину и разбил ее на треугольники (синяя). Вот разные варианты расчета ее деформации под собственным весом при разных закреплениях по границам (со скольжением (зеленая) и жесткое крепление (черная линии)):
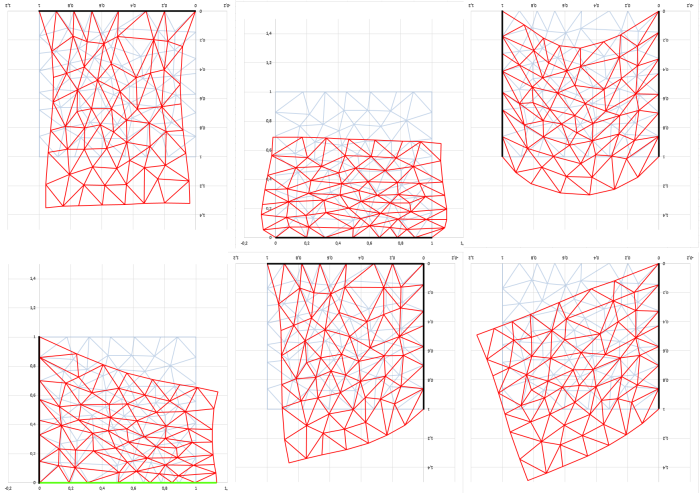
Я обнаружил для себя, что собственно расчет деформаций достаточно прост, несложный итерационный метод типа "двигай узел в сторону действия силы" быстро решает систему уравнений. А вот что оказалось сложнее, так это построение случайной треугольной сетки.
Сначала я заполнил квадратную область случайными точками так, чтобы расстояние между любой парой точек было не меньше заданного. При этом точки, попадающие близко к границе, "притягивались" к ней. Потом использовал жадный алгоритм, который ранжировал расстояния между всеми парами точек от самого короткого до самого длинного и начинал соединять по порядку самые близкие пары. При это контролировал пересечение создаваемого ребра со всеми уже имеющимися (если пересечение есть, ребро не строится). И наконец, алгоритм должен был найти все получившиеся треугольные элементы и выдать тройки их вершин.
Я в программировании слабо разбираюсь, все это делал в екселе. Но теперь явно вижу, что нужно освоить что-то более подходящее для подобных расчетов. В общем, ексель все это считает, конечно, и даже почти все делает автоматически. Я даже узнал, что такое формулы массива (очень полезно для таких вычислений).
Кстати, для решения системы уравнений деформаций я сначала использовал градиентный метод (в качестве целевой функции я взял сумму квадратов всех сил в узлах, которая должна быть равна нулю в равновесии). И он работал довольно необычно. Т.е. решение он находил, конечно, но его путь к этому решению выглядел контринтуитивно. Ты ожидаешь, что путь к решению будет выглядеть, как если бы к телу плавно прикладывали увеличивающуюся нагрузку (и метод типа "двигай узел в сторону действия силы" так примерно и двигается к решению). Но градиентный спуск делал нечто другое. Скажем, он не пытался переместить треугольный элемент, как единое целое, без деформаций, т.к. это не вело к изменению целевой функции. И если, скажем, закрепленное тело нагружается собственным весом, то градиентный метод вначале начинает "шевелить" треугольные элементы у закрепленного периметра, т.к. их невозможно двигать без деформации и они дают вклад в целевую функцию. Все остальные элементы далеко от заделки остаются неподвижными (пока "волна деформации" их не достигнет), хотя силы в их узлах действуют. В итоге тело двигается к конечному решению медленно и через какую-то странную последовательность непонятных изгибов, которые иногда выглядят совершенно не физично. Я даже вначале подумал, что расчет просто ошибочный.



