Задача на абберацию света

[Enceladoglu]

В некоторый момент времени направление луча света от звезды составляет угол $\theta$ с орбитальной скоростью $\mathbf{v}$ Земли ( в системе, связанной с Солнцем). Найти изменение направления от Земли на звезду за полгода (аберрация света), не делая приближений, связанных с малостью $\frac{v}{c}$

Решение в ответе:
Определение угла аберрации сводится к вычислению двух углов (см. рисунок): угла $\alpha_1$ между направлением луча $AC$ и направлением скорости $\mathbf{v}$ Земли в первом ее положении и угла $\alpha_2$ между направлением $BC$ луча и направлением скорости $\mathbf{v'}$ Земли во втором ее положении (через полгода). Угол аберрации можно определить как $\delta$ можно определить как $\delta = (\pi - \alpha_2) - \alpha_1 = \pi - \alpha_1 - \alpha_2$. Углы $\alpha_1$ и $\alpha_2$ вычислим по формуле $ \tg \theta = \frac{\sin \theta'}{\gamma (\cos \theta' + \beta)}$, выразив их через угол $\theta$(вероятно, это не тот же угол что и в формуле с тангенсом, корректней наверное написать тут формулу обратную к ней, $ \tg \theta' = \frac{\sin \theta}{\gamma (\cos \theta - \beta)}$), который наблюдается в системе отсчета, связанной с Солнцев, между лучом $OC$ света и вектором скорости Земли:
$\tg(\pi - \alpha_1) = \frac{1}{\gamma} \frac{\sin \theta}{\cos \theta - \beta}, \tg(\pi - \alpha_2) = -\frac{1}{\gamma} \frac{\sin \theta}{\cos \theta + \beta} $
Отсюда находим
$\tg \frac{\delta}{2} = \sqrt{\frac{1 - \cos \delta}{1 + \cos \delta}} = \beta \gamma \sin \theta$
Заметим, что все три угла между скоростями, изображенные на рисунке относятся к разным системам отсчета и что сам рисунок условен.


У меня вопрос лишь в том, что это за такие углы $\alpha_1$ и $\alpha_2$ ? Почему используют именно их ? $\alpha_1$ смежный угол, по отношению к углу между скоростью Земли и направлением на звезду, и его использование как-то не логично.

[svv]

Enceladoglu в сообщении #1656097 писал(а):

Почему используют именно их ?

Так делать не обязательно и, действительно, такой выбор углов на рисунке не вполне соответствует их описанию в тексте решения. Я думаю, автор стремился к тому, чтобы углы $\alpha_1, \alpha_2$ были внутренними углами треугольника, тогда $\delta=\pi-\alpha_1-\alpha_2$. Картинка тут не нужна. Она никак не помогает решению (а может быть, и запутывает, что видно по замечаниям автора о её условности).

Вот начало моего решения. Вводим ИСО: $S$ (Солнца), $S^+$ (Земли, когда она движется со скоростью $+\mathbf v$), $S^-$ (Земли, когда она движется со скоростью $-\mathbf v$). Ось $Ox$ направим вдоль $\mathbf v$, ось $Oy$ перпендикулярно ей, так, чтобы луч лежал в плоскости $Oxy$. Запишем преобразования Лоренца для компонент волнового вектора:
$\begin{array}{ll}k^+_x = \gamma(k_x-\beta\frac{\omega}{c}) & k^-_x = \gamma(k_x+\beta\frac{\omega}{c}) \\k^+_y = k_y & k^-_y = k_y\end{array}$
Учтём, что $\frac{\omega}{c}=k$. (Величины $\omega, k, k_x, k_y$ относятся к $S$.) Деля верхние формулы на нижние, получим
$\frac{k^+_x}{k^+_y}=\gamma\left(\frac{k_x}{k_y}-\beta\frac k{k_y}\right);\quad\frac{k^-_x}{k^-_y}=\gamma\left(\frac{k_x}{k_y}+\beta\frac k{k_y}\right)$

Угол $\theta$ определяется соотношениями
$\begin{array}{l}k_x = k\cos\theta\\k_y= k\sin\theta \end{array}$
Углы $\theta^+,\theta^-$ определим аналогично. Тогда
$\ctg\theta^+=\gamma(\ctg\theta-\beta\csc\theta);\quad \ctg\theta^-=\gamma (\ctg\theta+\beta\csc\theta)$
Это эквивалентно

Enceladoglu в сообщении #1656097 писал(а):

$\tg(\pi - \alpha_1) = \frac{1}{\gamma} \frac{\sin \theta}{\cos \theta - \beta}, \tg(\pi - \alpha_2) = -\frac{1}{\gamma} \frac{\sin \theta}{\cos \theta + \beta} $

[lazarius]

Enceladoglu в сообщении #1656097 писал(а):

$\alpha_1$ смежный угол, по отношению к углу между скоростью Земли и направлением на звезду

Это вряд ли. Описание очень мутное но попробуем примирить текст и рисунок.

Цитата:

направление луча света от звезды составляет угол $\theta$ с орбитальной скоростью $\mathbf{v}$ Земли

Если это от звезды, то в точке $O$ Земля движется направо (в системе покоя Солнца).

Цитата:

угла $\alpha_1$ между направлением луча $AC$ и направлением скорости $\mathbf{v}$ Земли в первом ее положении

Если это луч $AC$ (то есть от Земли к Солнцу), то и здесь Земля движется направо.

И только при таком движении рисунок становится правильным. Потому что так называемый headlight effect говорит нам что в системе, в которой источник движется, лучи сходятся в направлении движения.

Если в точке A направление луча показано в системе покоя Земли и, при этом, Солнце движется налево, то луч $CA$ как и положено отклоняется в сторону движения Солнца по сравнению с лучем $CO$ в системе покоя Солнца.

Итак чтобы примирить рисунок с текстом и физикой явления, достаточно маленькую стрелочку в точке $A$ понимать как направление движения Солнца.

В точке $B$ мы очевидно имеем то же самое - Солнце движется направо и луч $CB$ отклонен в сторону движения Солнца. Но для этого положения углом $\theta$ (в смысле первой цитаты) в точке $O$ будет тупой угол.

Формулы я не проверял.

[svv]

lazarius в сообщении #1656124 писал(а):

Описание очень мутное но попробуем примирить текст и рисунок.

Ключ к пониманию рисунка в том, что $C$ — не звезда, как хотелось бы думать. Звезда находится где-то далеко внизу, на прямой $OC$. Направления лучей:
$\vec{AC}$, когда Земля движется влево, со скоростью $\mathbf v$;
$\vec{OC}$, "когда стоит", т.е. в системе Солнца;
$\vec{BC}$, когда движется вправо, со скоростью $\mathbf v'=-\mathbf v$.
Ни Земли, ни Солнца на картинке нет, здесь изображены лишь скорости и направления.

[Ende]

Тема перемещена из форума «Физика» в форум «Помогите решить / разобраться (Ф)»
Причина переноса: темы, в которых нужно что-то объяснить или подсказать в пределах учебных курсов, создаются в этом разделе.

[lazarius]

svv в сообщении #1656150 писал(а):

Ключ к пониманию рисунка в том, что $C$ — не звезда, как хотелось бы думать.

И вроде бы стрелочки в точке C говорят об этом же. И я даже соглашусь с вами в том что тот кто делал рисунок имел ввиду именно это. Но тогда угол $\alpha_1$ на рисунке не является тем что написано в тексте так же как и угол $\alpha_2$. А в моей интерпретации все сходится - и формулы тоже. :)

[svv]

lazarius в сообщении #1656163 писал(а):

А в моей интерпретации все сходится - и формулы тоже. :)

Кроме мелочи — нет соответствия с текстом решения:
1) Авторы пишут, что $\mathbf v$ — это скорость Земли относительно Солнца, а мы говорим, что наоборот.
2) Авторы пишут про направление лучей $AC, BC, OC$, упорно ставя точку $C$ на второе место (и да, стрелочки на рисунке), а мы считаем наоборот.
Но я думаю, что

svv в сообщении #1656117 писал(а):

Картинка тут не нужна. Она никак не помогает решению (а может быть, и запутывает, что видно по замечаниям автора о её условности).

[lazarius]

svv в сообщении #1656167 писал(а):

1) Авторы пишут, что $\mathbf v$ — это скорость Земли относительно Солнца, а мы говорим, что наоборот.

Нет. $\mathbf v$ - скорость Земли относительно Солнца. Нигде не написано что стрелочка показывает в направлении $\mathbf v$. :)

svv в сообщении #1656167 писал(а):

2) Авторы пишут про направление лучей $AC, BC, OC$, упорно ставя точку $C$ на второе место (и да, стрелочки на рисунке), а мы считаем наоборот.

Нет. Мы просто под этими лучами понимаем чистую геометрию. :)

svv в сообщении #1656167 писал(а):

Но я думаю, что картинка тут не нужна. Она никак не помогает решению (а может быть, и запутывает, что видно по замечаниям автора о её условности).

Под условностью здесь понимается только то что рисунок является суперпозицией трех в разных системах отсчета.

Формулу для тангенса получают именно так как написано у вас - делением двух соотношений в преобразовании Лоренца для волнового вектора - параграф 3.7 Moving light sources, формула 3.70:

https://users.physics.ox.ac.uk/~Steane/ ... /rel_A.pdf

Запишем сразу с учетом того что у нас свет и не забываем что здесь $\beta$ - скорость источника:

$\displaystyle \tg\theta = \frac{\sin\theta_0}{\gamma(\cos\theta_0 + \beta)}$

Я не понимаю для чего каждый раз танцевать от печки, когда можно просто подставить в эту формулу правильные значения.

Для положения $A$ в оригинальной (вашей) интерпретации $\theta_0$ совпадает с $\theta$ на рисунке, $\theta$ в формуле - смежный с углом $\alpha_1$ на рисунке:

$\displaystyle \tg(\pi - \alpha_1) = \frac{\sin\theta}{\gamma(\cos\theta - \beta)}$

Для положения $B$ в оригинальной интерпретации $\theta_0$ также $\theta$ на рисунке, $\theta$ в формуле - $\alpha_2$ на рисунке:

$\displaystyle \tg\alpha_2 = \frac{\sin\theta}{\gamma(\cos\theta + \beta)}$

[svv]

lazarius в сообщении #1656177 писал(а):

Нигде не написано что стрелочка показывает в направлении $\mathbf v$. :)

А надписи $\mathbf v$ и $\mathbf v'=-\mathbf v$ возле стрелочек на рисунке просто так поставлены?

lazarius в сообщении #1656177 писал(а):

Под условностью здесь понимается только то что рисунок является суперпозицией трех в разных системах отсчета.

Авторы считают, что не только это:

То есть, хотелось бы, чтобы сложение векторов на рисунке соответствовало сложению скоростей, но в СТО так не получится, и, самое большее, можно считать, что вектор на рисунке соответствует скорости с коэффициентом, показывая правильно лишь её направление.

lazarius в сообщении #1656177 писал(а):

svv в сообщении #1656167 писал(а):

2) Авторы пишут про направление лучей $AC, BC, OC$, упорно ставя точку $C$ на второе место (и да, стрелочки на рисунке), а мы считаем наоборот.

Нет. Мы просто под этими лучами понимаем чистую геометрию. :)

Вот прямо с самого начала решения задачи у Вас это чистая геометрия? Но ведь выбор одного из двух противоположных направлений распространения света вдоль прямых важен. Если в ИСО Солнца задана прямая $CO$, то от того, в какую сторону ($CO$ или $OC$) распространяется вдоль неё свет, будет зависеть наклон прямой $CA$ в ИСО Земли. Вы же сами, вроде бы, об этом беспокоились:

lazarius в сообщении #1656124 писал(а):

Если в точке A направление луча показано в системе покоя Земли и, при этом, Солнце движется налево, то луч $CA$ как и положено отклоняется в сторону движения Солнца по сравнению с лучем $CO$ в системе покоя Солнца.

Имея в ИСО Солнца лишь прямую $CO$ («чистую геометрию»), без маленькой стрелочки на ней , Вы не построите прямую $CA$ в ИСО Земли.

[lazarius]

svv в сообщении #1656180 писал(а):

Авторы считают, что не только это

Ok! Сейчас когда вы дали screenshot я вижу что на рисунке схематично показаны две разности векторов отложенных от точки $O$.

И все-таки это не значит что "картинка не нужна." Углы это геометрия и рисунок не помешает.

[Enceladoglu]

lazarius в сообщении #1656220 писал(а):

Сейчас когда вы дали screenshot

Прошу прощение за то что я поленился уделить 5 секунд своего времени и не дописал информацию, которая как оказалось была существенной, в первом же сообщении

svv в сообщении #1656150 писал(а):

Ключ к пониманию рисунка в том, что $C$ — не звезда, как хотелось бы думать. Звезда находится где-то далеко внизу, на прямой $OC$

Вот это ключевое, и тут было мое непонимание рисунка, и отсюда выбора угла.
Направление на звезду противоположно направлению скорости света от звезды. А в формулах аберрации фигурирует именно угол между скоростями.


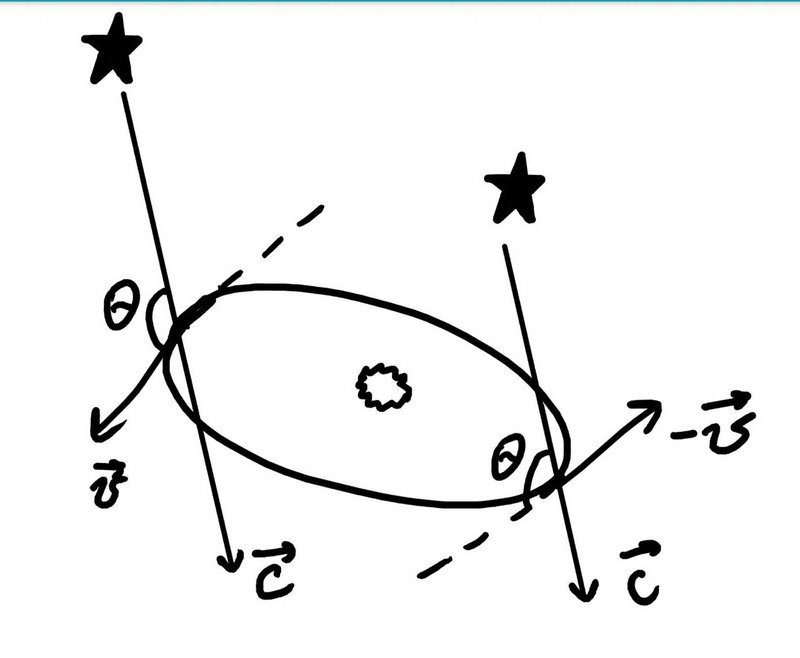
Сверху - в системе отсчета Солнца нарисованы два положения Земли, и направления на звезду.
Снизу слева - это углы в системе отсчета первого положения Земли
Снизу справа - это углы в системе отсчета второго положения Земли
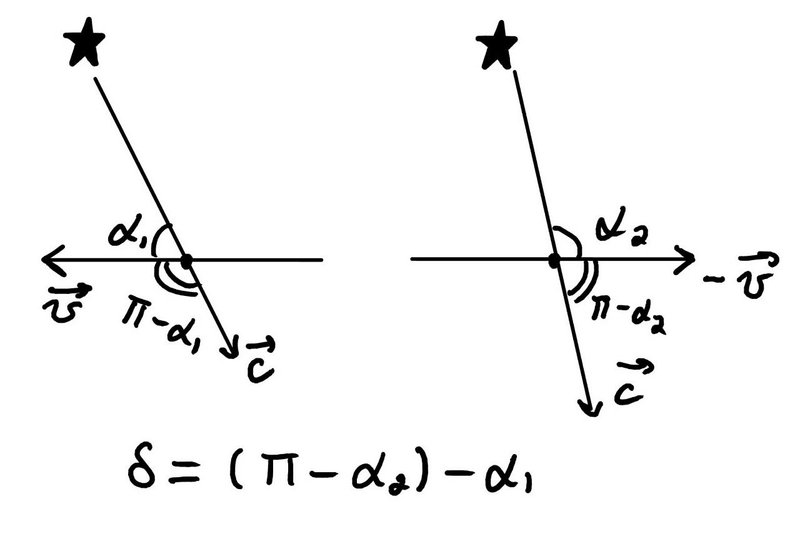
Если принять $\alpha_1$ и $\alpha_2$ углы между направлением на звезду, то выбор этих углов действительно выглядит естественным для этой задачи.
Но назвать их:

Цитата:

угла $\alpha_1$ между направлением луча $AC$ и направлением скорости $\mathbf{v}$

как то язык тогда не поворачивается..это звучит как угол между скоростями, но тогда вместо
$\tg(\pi - \alpha_1) = \frac{1}{\gamma} \frac{\sin \theta}{\cos \theta - \beta}, \tg(\pi - \alpha_2) = -\frac{1}{\gamma} \frac{\sin \theta}{\cos \theta + \beta} $
должны быть $\tg(\alpha_1), \tg(\alpha_2)$
Т.е. действительно если я правильно все понял то описание в тексте немного не соответствует обозначениям.
И там написано

Цитата:

В некоторый момент времени направление луча света от звезды составляет угол $\theta$ с орбитальной скоростью $\mathbf{v}$

Т.е. $\theta$ это вообще говоря смежный угол с тем $\theta$ что я нарисовал на рисунке, и имелся ввиду угол между скоростями..
вообщем, действительно мутно все это..

Я завис на тригонометрии при попытке получить выражение $\tg \frac{\delta}{2} = \beta \gamma \sin \theta$

$ \tg \frac{\delta}{2} = \tg \frac{\pi - \alpha_1 - \alpha_2}{2} = \tg \frac{(\pi - \alpha_1) + (\pi - \alpha_2) - \pi}{2} = \ctg \frac{(\pi - \alpha_1) + (\pi - \alpha_2)}{2} $ $ = \frac{1}{\tg \frac{(\pi - \alpha_1) + (\pi - \alpha_2)}{2}} = \frac{1 - \tg \frac{\pi - \alpha_1}{2} \tg \frac{\pi - \alpha_2}{2}}{\tg \frac{\pi - \alpha_2}{2} + \tg \frac{\pi - \alpha_2}{2}}$

Формула аберрацции для косинуса:
$ \cos \theta' = \frac{\cos \theta - \beta}{1 - \beta \cos \theta} $
Тогда
$ \cos (\pi - \alpha_1) = \frac{\cos \theta - \beta}{1 - \beta \cos \theta} $
$ \cos (\pi - \alpha_2) = \frac{\cos (\pi - \theta) - \beta}{1 - \beta \cos (\pi - \theta)} = -\frac{\cos \theta + \beta}{1 + \beta \cos \theta} $ (наверное)

$ \tg \frac{\pi - \alpha_1}{2} = \sqrt{\frac{1 - \cos (\pi - \alpha_1)}{1 + \cos (\pi - \alpha_1)}} = \sqrt{\frac{1 - \beta \cos \theta - \cos \theta + \beta}{1 - \beta \cos \theta + \cos \theta - \beta}} = \sqrt{\frac{(1 + \beta) (1 - \cos \theta ) }{(1 - \beta)(1 + \cos \theta ) }} $

$\tg \frac{\pi - \alpha_2}{2} = \sqrt{\frac{1 - \cos (\pi - \alpha_2)}{1 + \cos (\pi - \alpha_2)}} = $ $\sqrt{\frac{1 + \beta \cos \theta + \cos \theta + \beta}{1 + \beta \cos \theta - \cos \theta - \beta}} = \sqrt{\frac{(1 + \beta)(1 + \cos \theta)}{(1 - \beta)(1 - \cos \theta)}} $
$\tg \frac{\delta}{2} = \frac{1 - \frac{1 + \beta}{1 - \beta}}{(\tg \frac{\theta}{2} + \ctg \frac{\theta}{2})\sqrt{\frac{1 + \beta}{1 - \beta}}} = \frac{\frac{-2 \beta}{1 - \beta}}{\frac{1}{\sin \frac{\theta}{2} \cos \frac{\theta}{2}} \sqrt{\frac{1 - \beta^2}{(1 - \beta)^2}}} = -\beta \gamma \sin \theta $

[lazarius]

Enceladoglu в сообщении #1656379 писал(а):

Формула аберрацции для косинуса:
$ \cos \theta' = \frac{\cos \theta - \beta}{1 - \beta \cos \theta} $

Существует еще одна формула эквивалентная этой:

$\displaystyle \tg \frac{\theta^\prime}{2} = \sqrt \frac {1 + \beta}{1 - \beta} \tg \frac{\theta}{2}$

В обозначениях из первого сообщения svv:

$\displaystyle \begin{aligned}\tg\frac{\delta}{2} & = \tg\frac{\theta^+ - \theta^-}{2} = \frac{\tg\frac{\theta^+}{2} - \tg\frac{\theta^-}{2}}{1 + \tg\frac{\theta^+}{2}\tg\frac{\theta^-}{2}} \\ & = \left(\sqrt \frac {1 + \beta}{1 - \beta} - \sqrt \frac {1 - \beta}{1 + \beta}\right) \frac{\tg\frac{\theta}{2}}{1 + \tg^2\frac{\theta}{2}} = \beta\gamma\sin\theta \end{aligned}$

[Enceladoglu]

Я накосячил в прошлом рисунке

Я действительно все время считал, как и написано в условии задачи, что $\theta$ это угол именно между скоростями (в первом положении, и смежный между скоростями во втором)
Тоесть
$\theta \to \pi - \alpha_1$ в первом случае
$\pi - \theta \to \pi - \alpha_2$ во втором случае
Но это не отменяет того что

Цитата:

угла $\alpha_1$ между направлением луча $AC$ и направлением скорости $\mathbf{v}$ Земли в первом ее положении и угла $\alpha_2$ между направлением $BC$ луча и направлением скорости $\mathbf{v'}$ Земли во втором ее положении

вызывает несостыковку

lazarius в сообщении #1656408 писал(а):

Существует еще одна формула эквивалентная этой:
$\displaystyle \tg \frac{\theta^\prime}{2} = \sqrt \frac {1 + \beta}{1 - \beta} \tg \frac{\theta}{2}$

Ну, я их по факту и выводил тут

Enceladoglu в сообщении #1656379 писал(а):

$ \tg \frac{\pi - \alpha_1}{2} = \sqrt{\frac{1 - \cos (\pi - \alpha_1)}{1 + \cos (\pi - \alpha_1)}} = \sqrt{\frac{1 - \beta \cos \theta - \cos \theta + \beta}{1 - \beta \cos \theta + \cos \theta - \beta}} = \sqrt{\frac{(1 + \beta) (1 - \cos \theta ) }{(1 - \beta)(1 + \cos \theta ) }} $

$\tg \frac{\pi - \alpha_2}{2} = \sqrt{\frac{1 - \cos (\pi - \alpha_2)}{1 + \cos (\pi - \alpha_2)}} = $ $\sqrt{\frac{1 + \beta \cos \theta + \cos \theta + \beta}{1 + \beta \cos \theta - \cos \theta - \beta}} = \sqrt{\frac{(1 + \beta)(1 + \cos \theta)}{(1 - \beta)(1 - \cos \theta)}} $

Еще непонятно зачем авторы акцентировали внимание на

Цитата:

$\tg(\pi - \alpha_1) = \frac{1}{\gamma} \frac{\sin \theta}{\cos \theta - \beta}, \tg(\pi - \alpha_2) = -\frac{1}{\gamma} \frac{\sin \theta}{\cos \theta + \beta} $

Хотя я их по факту не использовал. Или с помощью них можно получит соотношение $\displaystyle \tg \frac{\theta^\prime}{2} = \sqrt \frac {1 + \beta}{1 - \beta} \tg \frac{\theta}{2}$ более легким путем ?

[svv]

Enceladoglu в сообщении #1656379 писал(а):

Я завис на тригонометрии при попытке получить выражение $\tg \frac{\delta}{2} = \beta \gamma \sin \theta$

$ \tg \frac{\delta}{2} = \tg \frac{\pi - \alpha_1 - \alpha_2}{2} = \tg \frac{(\pi - \alpha_1) + (\pi - \alpha_2) - \pi}{2} \stackrel{\color{magenta}\mathrm{???}}{=} \ctg \frac{(\pi - \alpha_1) + (\pi - \alpha_2)}{2} $ $ = \frac{1}{\tg \frac{(\pi - \alpha_1) + (\pi - \alpha_2)}{2}} = \frac{1 - \tg \frac{\pi - \alpha_1}{2} \tg \frac{\pi - \alpha_2}{2}}{\tg \frac{\pi - \alpha_2}{2} + \tg \frac{\pi - \alpha_2}{2}}$

Ошибка тут.

[Enceladoglu]

svv
Ну конечно
Спасибо большое !