Нуждаюсь в обсуждении и помощи в физической интерпретации эффектов, которыми я сейчас занимаюсь.
В общем случае произвольной проводимости

, волновое уравнение для электрического поля

в системе СИ имеет следующий вид:

Последний член в уравнении (1) отвечает за ток смещения. Второе слагаемое в этом уравнении отвественно за возникновение классического скин-эффекта. Пользуясь законом Ома

и решая уравнение (1) для цилиндрического проводника радиусом

, можно получить распределение плотности тока в поперечном сечении проводника в виде:

где

- плотность тока вдоль поверхности цилиндра;

- функция Бесселя первого рода нулевого порядка;

- отношение плотности тока смещения (

) к току проводимости (

);

- толщина скин-слоя при

;

- радиальная координата.
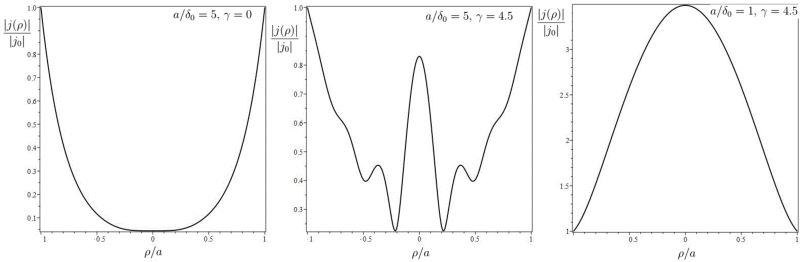
На рисунках ниже приведено распределение плотности тока по радиальной координате

при различных отношениях

и значениях

. Видно, что при существенной величине

это распределение приобретает "не классический" вид. В частности, (третий рисунок) возможно возникновение инверсного скин-эффекта, природа которого мне до конца не ясна и которую я хотел бы обсудить с форумчанами.