Я не вижу, что в Ваших рассуждениях сломается, если мы придумаем какой-то вычислимый способ записывать формулы, в котором любая битовая строка будет формулой, и на основании этого объявим, что язык

позволяет выразить что угодно.
Вы уверены, что хотели сказать именно про тот случай, когда
любая битовая строка является формулой? Это примерно то же самое, что приписать предложениям языка натуральные числа (а это делает любая грамматика). Тогда определение акиоматики сведется просто к определению множества чисел - аксиом, и определению числовых функций - правил вывода. Если эти функции - вычислимые, а множество аксиом - рекурсивно, то получится вполне нормальная теория, с которой можно работать, хотя и способ кодировки утверждений может быть неудобным для человеческого восприятия. И да, любую разумную теорию можно закодировать таким образом, так что "выразимость чего угодно" в таком смысле меня совершенно устраивает.
Если же Вы сказали это в смысле указания на бедность алфавита

и имели в виду, что на этом алфавите должна быть определена любая грамматика, то я ничего не имею против этого, если грамматика будет разрешимой. На таком языке не удастся "выразить что угодно" разве что в том случае, когда количество предложений окажется конечным. Или наоборот, если грамматика окажется неразрешимой.
Кстати, Ваш пример с интерпретацией символа

языка арифметики Пресбургера как символа принадлежности в теории множеств - не подходит, ибо

- функциональный символ, а принадлежность - предикат. Тем не менее, я согласен, что нестандартная интерпретация символа

(не как сложения) позволит определить в языке арифметики Пресбургера неразрешимую теорию.
Так товарищи утверждают, что не приписывают, а просто обнаруживают объективный факт.
Это ещё нужно посмотреть, что именно и в каком контексте утверждают товарищи. Но объективного факта, что среди естественных языков встречаются неразрешимые, очевидно, быть не может.
Разрешимые языки, не являющиеся контекстно зависимыми, точно существуют. Элементарно язык из пар

, таких что

- код МТ, останавливающейся на памяти

.
То, что существуют разрешимые языки, не являющиеся контекстно зависимыми, не вызывает сомнений. Я упомянул контекстно зависимые языки в том смысле, что это максимальный уровень в иерархии Хомского, к которому относятся гарантированно разрешимые языки.
Говоря про неограниченность естественных языков, указанные источники вряд ли имели в виду, что они являются разрешимыми, но не контекстно зависимыми, аналогично приводимому Вами примеру. Хотя, надо будет это внимательно посмотреть.
Да. Носитель модели плюс отображение из функциональных символов в функции, из предикатных в предикатные.
Так не получится - функция определена на натуральных числах, а в формулу подставляются термы.
Либо нужно сказать, что у нас к теории поставляется набор термов, обозначающих все натуральные числа. Но это уводит нас от просто языка совсем далеко.
Я понимаю, что числам нужно сопоставить замкнутые термы теории. И да, обычно это делается при построении модели в смысле теории моделей. Но мне не нужна полная интерпретация языка, обычно именуемая "моделью" заданной аксиоматики (ибо я всё равно считаю утверждение о существовании такой интерпретации неконструктивным надувательством). Мне достаточно доказательства того, что мы в состоянии записать формулу, которая в смысле предложенной нами аксиоматики и при условии интерпретации замкнутых термов (например, вида

,

,
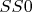
и т.д.) как чисел, корректно моделирует произвольную частично рекурсивную функцию.
В таком случае, почему вдруг множество теорем (не-абракадабр) неразрешимо? Возможно, я слишком узко представляю себе "теоремы"...
Речь о неполных (Гёдель называл их "достаточно содержательными") теориях. Остальные - мало интересны.
mihaild абсолютно верно отметил, что множество теорем (т.е. доказанных утверждений теории) формально тоже является языком. По иерархии Хомского этот язык относится как раз к неограниченным. В этом смысле теория (т.е. её аксиоматика) является той грамматикой, которая определяет этот язык. Так что понятия "грамматики" и "аксиоматики" являются в некотором смысле взаимозаменяемыми.
Тем не менее, отделять язык (грамматику) от теоретического содержания (аксиоматики), предложил как раз Ноам Хомский. Широко известен его пример грамматически коррекного, но содержательно бессмысленного предложения ("абракадабры", как Вы выразились): "Бесцветные зелёные идеи яростно спят". Хомский аргументировал, что грамматическая корректность этого набора слов заключается в том, что соответствующие части речи стоят "на правильных местах". Вообще-то это имеет значение только для английской грамматики, в русском языке порядок слов другой, да и в целом не имеет такого значения.
В русском языке имеют значение правильные словоформы (падежные и прочие окончания слов). Так что для русского языка тоже есть пример, который придумал Л.В. Щерба: "Глокая куздра штеко бодланула бокра и кудрячит бокрёнка". Предполагается, что несмотря на бессмысленность слов, нормальный русский способен грамматически проинтерпретировать это как предложение: Какая-то (прилагательное женского рода в именительном падеже) самка (субъект женского рода в именительном падеже) как-то (наречие, признак действия) воздействовала в прошлом на (глагол совершенной формы женского рода) самца (обьект мужского рода в винительном падеже) и (союз, играющий роль логической связки) в настоящее время воздействует на (глагол несовершенной формы) детёныша (объект мужского рода в уменьшительной форме винительного падежа).
Забавно, что к этой "грамматической интерпретации" тут же был придуман контрпример: "Шашлычная турка сильно обманула казака и дурачит казачёнка".
Так что в естественном языке грамматика на самом деле довольно причудливо перемешана с определениями понятий (т.е. с аксиоматикой). В частности "бессмысленное" предложение Ноама Хомского вполне может оказаться осмысленным в каком-то контексте, в котором определено, что значат "спящие идеи", как можно "яростно спать", в каком смысле можно говорить о цвете "идей" и при каких условиях "зелёное" можно назвать "бесцветным". Так что "осмысленность" зависит от аксиоматики. И тогда возникает вопрос: А зачем нам вообще нужны бессмысленные грамматически корректные предложения? Может быть сразу определять в качестве "грамматически корректного" только то, что утверждается теорией? Т.е. если нельзя утверждать бесцветность ничего зелёного, то может быть стоит признать пример Ноама Хомского "грамматически" некорректным?
И да, такой подход имеет право на существование. Однако он создаёт массу неудобств. Поэтому удобнее в качестве языка использовать только тот, распознавание предложений которого гарантированно завершается, причём достаточно быстро. И желательно не закладывать в него ничего такого, что не может быть принято всеми прикладными теориями. Например, в исчислении предикатов специфичным для языка теории является только т.н. "сигнатура" - конечный набор символов, который теория может использовать дополнительно к применяемым в логике. Вся остальная грамматика - общая для всех теорий, формализуемых в данной логике.