Задача 12 из задачника Вероятность в теоремах и задачах (с решениями) Книга 1, Ширяев, Эрлих, Яськов.
Надо доказать, что если

-- характеристическая функция, то функция

, вообще говоря, характеристической не является. В задачнике в качестве контрпримера приводится функция

, которая является характеристической для бернулиевской с.в., принимающей значения -1, 1 с вероятностями 1/2. Аргумент:
Функция  дифференцируема в нуле вплоть до второго порядка. Если бы функция
дифференцируема в нуле вплоть до второго порядка. Если бы функция  была характеристической, то согласно теореме 1 из Вероятность-I, гл. 2, §12 это бы означало, что она дифференцируема всюду, что, очевидно, не так.
была характеристической, то согласно теореме 1 из Вероятность-I, гл. 2, §12 это бы означало, что она дифференцируема всюду, что, очевидно, не так. Попытка. Пусть

. В теореме 1 доказываются семь основных свойств характеристических функций. Использую свойства 6 и 7. Свойство 6:
если существует и является конечной  , то
, то 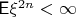 .
. Ясно, что

для любого

. Из неравенства Ляпунова следует, что

. Свойство 7 теоремы: если

для всех

, и верхний предел последовательности

равен

, где

, то характеристическая функция является аналитической на интервале

. В моем случае

и поэтому

- аналитическая на всей оси и, значит, дифференцируема в каждой точке.
Судя по написанному в задачнике, достаточно и того, что

дифференцируема в нуле вплоть до второго порядка. Как это доказать, не понимаю.