Потому, что мне ответ нужен.
Тут учебный раздел, в котором помогают изучающим физику разобраться в теме, подсказывая им пути решения. Давать прямые ответы запрещено правилами.
Прежде всего интересует вопрос: будет ли второй шарик проходить центральную точку?
В принципе, есть ещё и третий вариант: центральная точка - точка неустойчивого равновесия, и в такой идеализированной задаче второй шарик будет подбираться к ней бесконечно долго. Что там на самом деле - не знаю, нужно записать и линеаризовать уравнения движения. Законы сохранения такую возможность не запрещают.
А всевозможные лагранжианы в большинстве случаев не дают аналитических решений.
Всевозможные лагранжианы дают уравнения движения. Существует ли аналитическое решение, или уравнения движения можно проинтегрировать только численно - вопросы не к лагранжианам. Но иногда достаточно и уравнений движения, чтобы исследовать фазовые траектории системы и получить ответы на нужные вопросы.
В данном случае нет потенциальной энергии, так что, лагранжиан сводится к кинетической энергии, но, лучше, записанной в правильно выбранных обобщённых координатах, чтобы не связываться со связями. Применять ли к этой кинетической энергии уравнение Лагранжа, или воспользоваться законами сохранения - вопрос удобства.
Выберите в качестве обобщённых координат угол поворота первого стержня относительно вертикали и угол между двумя стержнями. В уравнения движения могут входить только эти две обобщённые координаты и две их производные по времени. Далее, ввиду центральной симметрии задачи сам угол поворота первого стержня не может входить в лагранжиан и влиять на динамику. Он не интересен, а его производную по времени при решении задачи нужно будет исключить. Дальше, у системы есть два закона сохранения: энергии и момента импульса. Запишите их для данных обобщённых координат. Закон сохранения момента импульса сразу дает уравнение для исключения производной первого угла по времени из закона сохранения энергии. И у вас останется нелинейное дифференциальное уравнение первого порядка для угла между стержнями. Исследуйте его.
И, да, перейдите с самого начала в единицы измерения, в которых
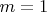
,

и

.



