Точки на концентрических окружностях

[denny]

На двух концентрических окружностях расположено $n$ и $m$ точек соответственно.
Для простоты вначале пусть они расположены в вершинах правильных $n$ и $m$ -угольников.
Мне надо так повернуть окружности относительно друг друга, чтобы оба множества были
максимально далеки по углам друг от друга. Ну как бы в "шахматном порядке".

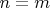
Если $n=m$ то идея очевидна -- располагаем точки одной окружности посередине (в смысле углов)
между точками другой.

Если $n \neq m$, то в любом случае сначала находим все попарные угловые расстояния
(с учетом $\mod 2\pi$).
И выбираем такой угол поворота, чтобы максимизировать минимальное расстояние.

У нас всего один параметр -- угол поворота, и мне кажется, для правильных многоугольников можно
найти точное решение (возможно, состоящие из нескольких ветвей, с модулями и т.п.)
Но что то я запутался ((

Ну и хотелось бы найти эффективный алгоритм, если точки заданы массивами углов.

[mihaild]

А от того, что окружности концентрические, а не одна и та же, что-то меняется? Вроде в обоих случаях важна только минимальная разность углов.

Если одно из множеств - правильный многоугольник с угловым размером стороны $\alpha$, а у другого угол $i$-й вершины $\beta_i$, то просто считаем все $\beta_i \mod \alpha$, берем из них минимум и максимум и соответственно поворачиваем.

[denny]

mihaild в сообщении #1644725 писал(а):

А от того, что окружности концентрические, а не одна и та же, что-то меняется? Вроде в обоих случаях важна только минимальная разность углов.

Нет конечно, просто так представлять удобнее
Спасибо, я все пытался формулы написать, но видимо так и надо делать

[dgwuqtj]

Для произвольных многоугольников есть алгоритм со сложностью $O(m n \log(m n))$. Просто ставим многоугольники как попало так, чтобы у них совместились какие-то две вершины. Для каждого такого положения можно посчитать такое следующее положение (при повороте одного из многоугольника в фиксированную сторону) за $O(\log(m n))$ с помощью подходящей структуры данных типа двоичной кучи, ну и предподсчёт за $O((m + n) \log(m n))$. Между двумя такими последовательными положениями порядок между вершинами многоугольников фиксирован, а максимум расстояний по углам достигается в точности посередине между ними.

Если многоугольники правильные, то все такие вырожденные положения изоморфны и всё считается за время предподсчёта.

[denny]

Нашел замкнутое выражение для правильных $n$ и $m$-гонов:

$$\pi \dfrac{\gcd(n,m)}{n m}$$