Да! я тоже делал через постоянство кривизны и ссылался на теорему Бельтрами. Есть ещё одно локальное доказательство постоянства кривизны, несколько более геометрическое, но тоже не сильно короткое (я когда-то напишу подробнее, наверно).
Давайте я напишу наконец "геометрическое" доказательство теоремы Бельтрами, которое придумал Владимир Матвеев; хотя я всё ещё надеюсь, что удастся обойтись без этой теоремы.
Теорема Бельтрами: если на связной гладкой поверхности

есть 2 римановы метрики, у которых геодезические одинаковые с точностью до перепараметризации, и при этом кривизна одной из метрик постоянна, то кривизна другой метрики тоже постоянна.
План доказательства:
- Замечаем, что поверхность
 имеет постоянную кривизну
имеет постоянную кривизну  любой касательный вектор можно локально продолжить до векторного поля Киллинга.
любой касательный вектор можно локально продолжить до векторного поля Киллинга. - Хотим по 2 римановым метрикам
 и
и  на
на  построить линейный автоморфизм
построить линейный автоморфизм  , переводящий
, переводящий  -поля Киллинга в
-поля Киллинга в  -поля Киллинга. Для этого используем такую характеризацию: векторное поле
-поля Киллинга. Для этого используем такую характеризацию: векторное поле  на римановом многообразии киллингово
на римановом многообразии киллингово  соответствующая 1-форма
соответствующая 1-форма  инвариантна относительно геодезического потока. (Знатоки заметят, что
инвариантна относительно геодезического потока. (Знатоки заметят, что  -- это сохраняющийся заряд, соответствующий
-- это сохраняющийся заряд, соответствующий  по теореме Нётер.)
по теореме Нётер.) - По
 (опускание индекса при помощи
(опускание индекса при помощи  ) очевидным образом строится инвариант геодезического потока
) очевидным образом строится инвариант геодезического потока  метрики
метрики  вида
вида  для не зависящего от
для не зависящего от  линейного автоморфизма
линейного автоморфизма  .
.
Проблема в том, что функция  не обязательно
не обязательно  -инвариантна, и поэтому
-инвариантна, и поэтому  не обязательно
не обязательно  -килингово. Но если удастся найти
-килингово. Но если удастся найти  -инвариантную функцию
-инвариантную функцию  вида
вида  для некоторой функции
для некоторой функции  (
( -- проекция), тогда
-- проекция), тогда  будет
будет  -киллингово, то есть
-киллингово, то есть  -- искомый автоморфизм
-- искомый автоморфизм  .
. - Вспоминаем, что геодезический поток гамильтонов. Замечаем, что любому сохраняющему траектории диффеоморфизму 4-мерных гамильтоновых систем соответствует некоторый инвариант.
- Вычисляем этот инвариант для нашего случая и убеждаемся, что он имеет нужный вид;
 .
.
Теперь подробности. (Все многообразия и функции по умолчанию подразумеваются гладкими.)
1. Если

-- связная поверхность постоянной кривизны, то (с точностью до умножения метрики на положительное число) она локально изометрична сфере

, евклидовой плоскости или плоскости Лобачевского. Касательный вектор

, отложенный от точки

на сфере, можно продолжить до генератора поворота воркуг оси, ортогональной

и

, а на плоскости Евклида или Лобачевского -- до генератора параллельного переноса в направлении

. Обратно, если любой

продолжается до киллингова поля

, то поток

задаёт, для любого достаточно малого

, изометрию

, где

-- окрестность

,

-- окрестность

; так как близкие точки можно соединить геодезической, то кривизна

постоянна.
2. Пусть

-- риманово многообразие. Для

обозначим

и

его вертикальное и горизонтальное поднятие соответственно (векторные поля на

, определённые вдоль

).

действует на функции

по формуле

; здесь

. А

вычисляет ковариантную производную; в частности, для 1-формы

на

верно

, и это однозначно определяет

; здесь

, а

в левой части понимается как функция

.
Генератор геодезического потока -- это векторное поле

на

, определяемое условием

; здесь индекс

означает, что берётся значение векторного поля в точке

. Пусть

-- векторное поле на

, тогда

. То есть осталось доказать, что

киллингово


-- кососимметрический тензор.
Продолжим произвольный

до локального векторного поля

на

, ковариантно постоянного в

. Тогда в точке


(т. к.

)
![$=g([X,Y],X)$ $=g([X,Y],X)$](https://dxdy-04.korotkov.co.uk/f/b/4/1/b4172f8d427119a1c25e6319c79274ee82.png)
(т. к.

без кручения)

(свойство коммутатора)
![$=-\frac12[L_Y(g(X,X))-(L_Yg)(X,X)]$ $=-\frac12[L_Y(g(X,X))-(L_Yg)(X,X)]$](https://dxdy-01.korotkov.co.uk/f/8/2/a/82a5af966b924c0f9f32fa79ca178d6682.png)
(правило Лейбница для производной Ли)

(т. к.

ковариантно постоянно).
Если

киллингово, то это

; и наоборот, поскольку

произволен и

симметрична.
3. Пусть на многообразии

2 римановы метрики

и

и

--

-поле Киллинга, то есть

инвариантна относительно геодезического потока

метрики

. Совпадение непараметризованных геодезических

и

означает, что диффеоморфизм

,

переводит траектории

на траектории

. Поэтому функция
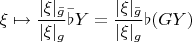

-инвариантна, где

; это равносильно

-инвариантности

, так как


-инвариантна
4. Пусть

-- симплектическое многообразие,

-- гладкая функция,

-- регулярное значение

. Обозначим

соответствующее гамильтоново векторное поле на

,

,

. Пусть

-- аналогичный набор данных (

),

-- диффеоморфизм, переводящий траектории потока

на траектории потока

(без учёта параметризации),

.
Так как

по определению невырожденна и кососимметрична, то

-- распределение ранга 1. Можно сказать точнее: так как

постоянен на

, то

для всех

, поэтому

(распределение, натянутое на наше гамильтоново векторное поле). Аналогично,

, а поскольку

сохраняет траектории, то

, поэтому

, так что

и

индуцируют невырожденные кососимметричные билинейные формы

и

на

. Так как

и

ещё и замкнуты как ограничения замкнутых форм, то они

-инвариантны по формуле Картана

.
Теперь пусть

. Тогда

, поэтому

и

отличаются на

-инвариантную функцию

. Если

и

пробегают какие-то открытые интервалы, то таким образом получается

-инвариантная функция на открытом подмножестве

.
5. Теперь

,

-- симплектическая форма на

, связанная с метрикой

(то есть

,

, где

,

),

-- гамильтониан геодезического потока

метрики

,

-- генератор

,

,

-- аналогичные вещи, связанные с метрикой

,

определён в п. 3. Вычислим инвариант

для этого случая.
Зафиксируем

,

и выберем

т. ч.

. В точке


(см. выше), а

(в стандартной римановой метрике

на

, относительно которой горизонтальное подпространство ортогонально вертикальному, а метрика на горизонтальном и на вертикальном индуцирована с

); действительно,

вертикален, так как

постоянен вдоль геодезических, а


для любого

. Поэтому в точке


.
Продолжим

до векторного поля около

; продолжение будем обозначать тоже

, обозначим также

,

. В точке

![$\omega(v,w)=(d\theta)(v,w)=v(\theta(w))-w(\theta(v))-\theta([v,w])=v(\theta(w))$ $\omega(v,w)=(d\theta)(v,w)=v(\theta(w))-w(\theta(v))-\theta([v,w])=v(\theta(w))$](https://dxdy-04.korotkov.co.uk/f/f/1/d/f1d22090cdbd9d0d09bf8b75658f4dfb82.png)
(так как по определению

на вертикальных векторах;
![$[v,w]$ $[v,w]$](https://dxdy-03.korotkov.co.uk/f/e/a/f/eaf55368264516205ef760de542c017682.png)
вертикально, поскольку
![$\pi_*[v,w]=[0,\eta]=0$ $\pi_*[v,w]=[0,\eta]=0$](https://dxdy-02.korotkov.co.uk/f/9/a/e/9ae4179fa6c7f10c94f55f75975faf9c82.png)
)

.
Аналогично, в точке

получаем

. Пусть

, тогда


. Вычислим производную этой функции переменной

вдоль векторного поля

в точке

:


(использовали правило дифференцирования произведения и частного)

(использовали

)

.
Так как

, то

, поэтому

.
Из инвариантности

и

следует, что функция

тоже инвариантна относительно геодезического потока

, что согласно п. 3 плана доказывает теорему Бельтрами.