Таблица с целыми числами

[Edward_Tur]

Таблица $3\times7$ заполнена целыми числами. Доказать, что можно удалить 3 столбца так, чтоб в оставшейся таблице $3\times4$ суммы чисел в каждой строке были четными.

[iifat]

(Оффтоп)

Поскольку интересует только чётность, заменим чётные числа на ноль, нечётные на единицу. Каждый столбец, таким образом, состоит из трёх двоичных разрядов, что соответствует числам от $0$ до $7$. Сумма столбцов исходной задачи соответствует побитовому сложению, то бишь, тоже от $0$ до $7$. Пар столбцов в таблице $C_7^2=21$, то бишь, обязаны найтись две пары с одинаковой чётностью сумм. Вот эти две пары, четыре столбца, оставляем, прочее вычёркиваем.

[iifat]

(Оффтоп)

И нет. Пары могут пересекаться. Ерунда. Правда, каких-то совпадающих пар непременно будет три, но образованы они могут быть тремя столбцами.

[TOTAL]

Если различных столбцов более пяти, то найдутся две различные пары антиподов.
Если различных столбцов менее пяти, то найдутся две различные пары близнецов.

Остаётся случай с тремя нулевыми столбцами, одним единичным и тремя смешанными.
Сумма трёх смешанных столбцов равна: одному из них, близнецу одного из них, нулевому, единичному.
В каждом случает понятно, что делать.

[TOTAL]

Ещё упустил случай с тремя нулевыми и четырьмя смешанными (среди которых есть пара антиподов). Тоже легко разруливается.

[lel0lel]

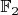
Рассмотрение над полем $\mathbb{F}_2$. Понятно, что нужно найти вектор столбец с четырьмя единичками и остальными нулевыми компонентами, проживающий в ядре соответствующего линейного оператора. Предположение, что такого вектора нет приведёт к противоречию.

Выбираются из ядра четыре линейно независимые вектора. Расположив их в строках, получается матрица $B\in \mathbb{F}_2^{4\times 7}$. Применяя к этой матрице метод Гаусса по строкам (это не выведет вектор-строки матрицы из ядра), можно получить четыре линейно независимые столбца с единственной единичкой и остальными нулями. Для удобства, переставляя эти столбцы, можно сформировать новую матрицу $\tilde{B}\in \mathbb{F}_2^{4\times 7}$, у которой левый блок -- единичная матрица $4\times 4$. Далее, следует работать только со строками $\tilde{B}$, тогда обратной, к сделанной ранее, перестановкой столбцов вернёмся к матрице с вектор-строками из ядра. Правый блок в $\tilde{B}$ -- матрица размерности $4\times 3$. Он не может иметь строк с тремя единичками, иначе получается строка с $4$ единичками, а это противоречие. Он также не может иметь более одной строки с двумя единичками на несовпадающих позициях, иначе сумма соответствующих строк в $\tilde{B}$ будет строкой с $4$ единичками. Аналогично, не может иметь более одной строки с одной единичкой на несовпадающих позициях. Не может иметь более двух строк с одной единичкой на совпадающих позициях (сумма опять даёт противоречие). В общем, у правого блока матрицы ${\tilde B}$ совсем мало возможностей и все они приводят к появлению строки с четырьмя единицами. В качестве примера ${\tilde B}$:
$\left( \begin{array}{ccccccc} 1 & 0 & 0 & 0 & {\bf 1} & {\bf 1} & {\bf 0} \\ 0 & 1 & 0 & 0 & {\bf 1} & {\bf 0} & {\bf 0} \\ 0 & 0 & 1 & 0 & {\bf 1} & {\bf 1} & {\bf 0} \\ 0 & 0 & 0 & 1 & {\bf 1} & {\bf 1} & {\bf 0} \\ \end{array} \right)$
В этом случае сумма трёх последних строк даёт противоречие.

[TOTAL]

Укорочу своё решение.
Если нет трёх одинаковых столбцов, то найдутся две пары близнецов или две пары антиподов.
Если есть три одинаковых столбца, то считаем их нулевыми, а из остальных четырёх столбцов составляем нетривиальную комбинацию равную нулевому столбцу.