Задача про построение циркулем и линейкой

[Eiktyrnir]

Здравствуйте уважаемые форумчане!
Помогите решить/разобраться.
Задача. Дана трапеция $ABCD$ с основанием $AB$ и $CD$. На отрезке $AB$ отмечена точка $E$. С помощью циркуля и линейки постройте точку $F$ на отрезке $CD$ так, чтобы площадь пересечения треугольников $ABF$ и $CDE$ была максимально возможной. (То есть опишите и обоснуйте алгоритм построения точки $F$ по данному расположению остальных точек).
Мои попытки решения.
1. Допустим $AB$ это верхнее основание трапеции (меньшее), а $CD$ это нижнее основание трапеции (большее). Мы вольны расположить точку $E$ как нам заблагорассудится, значит расположим ее посередине основания $AB$.
2. Тогда располагая $F$ различными способами на основании $CD$ мы будем получать треугольники $AFB$ и $DEC$ чьи площади кстати соотносятся как основания трапеции ($\frac {S_{AFB}} {S_{DEC}}=\frac {AB} {CD}$).
3. При пересечении треугольников $ABF$ и $CDE$ будут всегда получаться четырехугольники. Площадь произвольного четырехугольника есть $S=\frac {1} {2} d_{1}d_{2}\sin\alpha$.
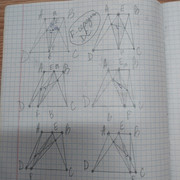
4. Я построил таким образом несколько таких пересечений треугольников $ABF$ и $CDE$ и увидел (пока чисто визуально), что максимальная площадь получается, если $F$ является ровно серединой основания $DC$. Конечно же построить середину отрезка при помощи циркуля и линейки проще простого и как его построить я Вас не спрашиваю (это тривиальное построение). Но я хочу спросить а как доказать то, что полученный таким образом четырехугольник будет иметь максимальную площадь не основываясь на "зрении"?

[svv]

Eiktyrnir в сообщении #1638083 писал(а):

4. Я построил таким образом несколько таких пересечений треугольников $ABF$ и $CDE$ и увидел (пока чисто визуально), что максимальная площадь получается, если $F$ является ровно серединой основания $DC$.

Так получилось потому только, что Вы взяли в качестве точки $E$ середину отрезка $AB$. При другом выборе так уже не получится. Но и в общем случае условие максимальности площади простое. Это некая пропорция.

Eiktyrnir в сообщении #1638083 писал(а):

Мы вольны расположить точку $E$ как нам заблагорассудится, значит расположим ее посередине основания $AB$.

Конечно, на чертеже Вам придётся выбрать какое-то конкретное расположение $E$. Но по условию точка $E$ дана, мы её положение не выбираем. Она может располагаться где угодно между $A$ и $B$. Так что в задаче надо рассмотреть общий случай.

[Eiktyrnir]

Цитата:

Так получилось потому только, что Вы взяли в качестве точки $E$ середину отрезка $AB$. При другом выборе так уже не получится. Но и в общем случае условие максимальности площади простое. Это некая пропорция.

1000 извинений. Пропорция между чем и чем?

Цитата:

Конечно, на чертеже Вам придётся выбрать какое-то конкретное расположение $E$. Но по условию точка $E$ дана, мы её положение не выбираем. Она может располагаться где угодно между $A$ и $B$. Так что в задаче надо рассмотреть общий случай.

Ох с этим совсем туговато...

[svv]

$AE:EB=DF:FC$ — это условие максимальности в общем случае. Но... его-то и надо получить
В частном случае $AE=EB$, который на Вашем чертеже, будет $DF=FC$, что Вы и увидели.

[Eiktyrnir]

svv в сообщении #1638301 писал(а):

$AE:EB=DF:FC$ — это условие максимальности в общем случае. Но... его-то и надо получить
В частном случае $AE=EB$, который на Вашем чертеже, будет $DF=FC$, что Вы и увидели.

Огромное спасибо, многоуважаемый!!!