@VAL: this argument can be refined slightly, since both
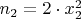
and
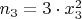
, the quadratic residues mean that any prime

dividing

must be of form
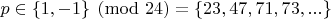
.
For
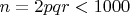
, I find that this immediately gives
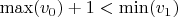
for

in (54, 90, 126, 150, 198, 210, 234, 250, 294, 306, 330, 342, 390, 414, 462, 522, 546, 558, 666, 738, 774, 846, 954), while there are still some values that need explicit testing for

in (350, 490, 510, 550, 570, 650, 686, 690, 714, 726, 770, 798, 850, 858, 870, 910, 930, 950, 966). Always assuming that my code to check these is correct.
Приведу доказательство того, что
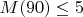
.
Возможно, это кому-то интересно. Но даже если не интересно, все равно, приведу, в надежде, что меня проверят. Ну и чтобы доказательство не потерялось (как у меня бывало с доказательствами на бумажке).
Я буду придерживаться фактов и обозначений из
Теоремы 1 (в этой ситуации доказательство будет совсем коротким).
Согласно этой теореме, если числа
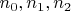
и
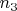
имеют по 90 делителей, то

кратно 3 и 5. Кроме кого, оно кратно 8. Чтобы у него оказалось 90 делителей оно должно иметь вид
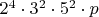
, или
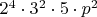
или
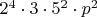
или вовсе не зависеть от параметра

.
В то же время,
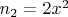
для некоторого нечетного

. Тогда
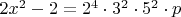
(или другому возможному варианту

).
Отсюда
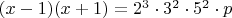
. НОД чисел

и

равен 2. Отсюда
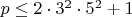
. И проверка свелась к короткому конечному перебору.
Остальные варианты (и остальные числа из
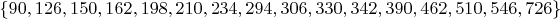
) проверяются аналогично (включая 162, для которого на показатель двойки у

не хватит одного простого делителя).
Надеюсь, что нигде не соврал. А если соврал, остается надеяться, что меня поймают за руку.