Как сконструировать предел по произведению?

[EminentVictorians]

Довольно легко показать полноту в малом категории $\mathbf{Set}$.

Возьмем произвольную (малую) категорию $J$ и сконструируем по ней её дискретный аналог $J_0$ (т.е. просто выкинем все стрелки, кроме единичных, а объекты оставим прежними). Легко показать, что для любого функтора $F: J_0 \to \mathbf{Set}$ существует $\operatorname{Lim} F$. Это будет просто самое обычное декартово произведение $\prod\limits_{i \in J_0}^{} F_{i}$ множеств $F_i$, индексированных объектами дискретной категории $J_0$.

Здесь я чуть-чуть отвлекусь и напомню, что декартово произведение множеств - оно всегда декартово произведение какой-то функции (т.е. функтора из дискретной индексирующей категории типа $J_0$). Даже когда говорят про декартово произведение $A \times B$ каких-то двух множеств и подразумевают под этим просто множество упорядоченных пар $(a, b)$ (где $a \in A, b \in B$), то все равно желательно помнить, что эта конструкция с парами - довольно частная и плохообобщаемая. Разумнее сразу понимать под декартовым произведением $A \times B$ не декартово произведение множеств $A$ и $B$, а декартово произведение функтора $f: 2 \to \mathbf{Set}$, такого, что $f(0) = A$, $f(1) = B$. Здесь $2$ - это дискретная категория (т.е. по сути просто множество), состоящая из каких-то двух объектов: 0 и 1. Тогда и само декартово произведение будет состоять не из упорядоченных пар $(a, b)$, а из функций вида $m: 2 \to A \cup B$ таких, что $m(0) \in A$ и $m(1) \in B$. Хорошее свойство этой конструкции (по сравнению с парами) заключается в том, что с её помощью можно определить декартово произведение любого семейства (в том числе и несчетного) множеств, в то время как через упорядоченные пары можно определить разве что декартово произведение двух множеств (даже для декартова произведения $n$ множеств уже нужны упорядоченные $n$-ки, не говоря уже о декартовом произведении бесконечного числа множеств).

Вернемся к общей конструкции. Как мы выяснили, декартовым произведением функтора $F: J_0 \to \mathbf{Set}$ будет являться множество функций вида

$$m: J_0 \to \bigcup\limits_{i \in J_0}^{}F_i$$

таких, что $m(i) \in F_i$
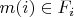
(здесь $F_i$ - это просто сокращенная запись для $F(i)$).

По сути, $m$ - это просто функция, выбирающая по элементу из каждого множества $F_i$ (именно поэтому, для того, чтобы доказать, что декартово произведение семейства непустых множеств не пусто, необходимо привлекать аксиому выбора). Поэтому, можно отождествить любую такую функцию $m$ с конусом $m$ (обозначу его точно так же, т.к. нет смысла вводить новое обозначение), нарисованным в категории $ \mathbf{Set}$, с вершиной в одноточечном множестве $*$ и стрелками $m_i: * \to F_i$ (каждая такая стрелка - это просто функция из одноточечного множества, а значит попросту выбор элемента в множестве $F_i$). В виду того, что категория $J_0$ дискретна, каждый такой конус $m$ является естественным преобразованием вида $m: (\Delta *) \dot{\to} F$, где $\Delta *: J_0 \to \mathbf{Set}$ - это диагональный (т.е. другими словами тождественный) функтор нашего одноточечного множества $* \in \mathbf{Set}$.

Тем самым, мы получаем, что наше декартово произведение $\prod\limits_{i \in J_0}^{} F_i = \operatorname{Lim} F$ функтора $F: J_0 \to \mathbf{Set}$ - это в точности множество естественных преобразований вида $(\Delta *) \dot{\to} F$:

$$\prod\limits_{i \in J_0}^{} F_i = \operatorname{Lim} F = \mathbf{Nat} [(\Delta *) \dot{\to} F]$$

Но ведь любой предел - это не просто объект, а целая универсальная стрелка. В нашем случае для функтора $F: J_0 \to \mathbf{Set}$ пределом будет являться не просто множество $ \operatorname{Lim} F$, а целая универсальная стрелка $p: \Delta \operatorname{Lim} F \to F$ в категории $\mathbf{Set}^{J_0}$ (функторов из $J_0$ в $\mathbf{Set}$). Т.е. естественное преобразование. Несложно понять, что роль естественных стрелок будут выполнять проекции нашего декартова произведения $\operatorname{Lim} F$:

$$p_i: \operatorname{Lim} F \to F_i$$

$$p_i (m) = m_i(*)$$

А что если теперь взять не дискретную категорию $J_0$, а произвольную категорию $J$, с которой мы и начинали. И вместо дискретного функтора $F: J_0 \to \mathbf{Set}$ возьмем уже (вообще говоря, не дискретный) функтор $G: J \to \mathbf{Set}$. Не уменьшая общности можно считать, что функтор $G$ просто продолжает функтор $F$ на появившиеся стрелки. Попробуем построить $ \operatorname{Lim} G$. Как мы уже выяснили, $ \operatorname{Lim} F$ - это множество конусов типа $m$, о которых речь шла выше. Может быть взять просто $ \operatorname{Lim} F$ в качестве кандидата на $ \operatorname{Lim} G$? Понятно, что так не получится: $ \operatorname{Lim} F$ не будет удовлетворять универсальному свойству предела для функтора $G$. Проблема в том, что конус (универсальная стрелка) $p: \Delta \operatorname{Lim} F \to G$ не обязан быть универсальным для функтора $G$. Он не обязан коммутировать со стрелками $G(u)$ - образами стрелок $u:j \to k$ из категории $J$ (которых до этого не было). Проблема коренится в конусах $m \in \operatorname{Lim} F$, которые не коммутируют со стрелками $G(u)$. Но категория $\mathbf{Set}$ хороша тем, что из любого множества можно выкинуть лишние элементы и получить при этом тоже множество. Возьмем и выкинем из $\operatorname{Lim} F$ ненужные нам конусы (те, которые не коммутируют со стрелками $G(u)$). В итоге получим множество $\operatorname{Lim} G$, которое и будет искомым пределом функтора $G$. А его проекциями будут все те же проекции, которые были в старом добром декартовом произведении (точнее, сужения тех проекций на новый домен $\operatorname{Lim} G$). Так и заканчивается доказательство полноты в малом категории $\mathbf{Set}$.

В итоге получаем аналогичную формулу

$$\operatorname{Lim} G = \mathbf{Nat} [(\Delta *) \dot{\to} G]$$

что и выше.

Очевидно, что привязываться к категории $\mathbf{Set}$ не надо. Интуиция очень уверенно подсказывает, что вот так построить предел из произведения можно в достаточно широком классе категорий. Что нам надо было, чтобы построить предел в $\mathbf{Set}$? По сути, реально играли роль 3 вещи:

1)Произведение $\prod\limits_{i \in J_0}^{} F_i$
2)Одноточечное множество $*$
3)Возможность "выкидывания" лишних вещей.

Понятно, что в совсем любой категории из просто существования произведений не будет вытекать существование пределов. Нужно что-то еще, по типу вот этого самого одноточечного множества в категории множеств, и по типу вот этой идеи с выкидыванием лишних элементов. Относительно выкидвания элементов, то это очень похоже на подобъекты и уравнители, здесь есть шанс все красиво описать в категорных терминах. Но вот какой будет аналог одноточечного множества? Терминальный объект? Но это слишком жестко получается, нужно что-то помягче.

Вопрос:
Есть ли инвариантное категорное описание этой идеи с одноточечным множеством? Её хочется использовать, чтобы строить пределы по произведениям в разных категориях, а не только в $\mathbf{Set}$.

[dgwuqtj]

Есть же стандартная теорема, что категория $\mathcal C$ имеет все малые пределы тогда и только тогда, когда в ней есть все малые произведения и уравнители. Доказательство вполне себе конструктивно (и сводится к $\mathbf{Set}$ через лемму Йонеды). Если же хочется чего-то в духе формулы с $\mathbf{Nat}$, то для этого в $\mathcal C$ нужны для начала внутренние $\mathrm{Hom}$-объекты (пусть и не все), то есть замкнутость, а это уже редкость...

[EminentVictorians]

dgwuqtj в сообщении #1632251 писал(а):

Есть же стандартная теорема, что категория $\mathcal C$ имеет все малые пределы тогда и только тогда, когда в ней есть все малые произведения и уравнители.

Я её и пытаюсь доказать. Доказательство Маклейна я не понимаю (и оно мне вообще не нравится, если честно). Я попытался вычленить существенные моменты из случая с $\mathbf{Set}$, но довести все до ума у меня не получается. Не знаете, есть какое-нибудь более ясное доказательство, чем у Маклейна? Пусть даже хотя бы просто на уровне идеи.

[dgwuqtj]

Не знаю насчёт принципиально другого доказательства, но можете посмотреть в книге Букур, Деляну, Введение в теорию категорий и функторов, глава 3, параграф 2. Возможно, там приятнее написано.

-- 08.03.2024, 23:46 --

Можно, конечно, легко свести утверждение к частному случаю пределов по конечным диаграммам.