p_n>4n

[qwert129]

Пусть $p_n$ это $n$-ное простое число. Найдите наименьшее k, для которого верно неравенство $p_n>4n$ для всех натуральных $n\ge k$ и докажите это неравенство.

(Я хотел доказать по индукции, но ничего не получилось, хотелось бы увидеть элементарное доказательство без теоремы о простых числах)

[EUgeneUS]

Разница $s_n=p_n-4n$ с ростом $n$ может уменьшаться только в одном случае - на паре простых чисел-близнецах. И уменьшается на $2$ в этом случае.
Если разница между соседними простыми равна $4$, то сумма не изменяется. А если больше, то увеличивается:

$$s_{n+1} - s_n = p_{n+1} - p_n - 4$$

Таким образом, нужно доказать, что при достаточно большом номере $n$ на каждую пару простых чисел близнецов найдется проруха пара соседних простых чисел с разницей больше $4$.

[мат-ламер]

Если разбить множество натуральных чисел на группы по 24 числа в каждой группе, то окажется, что в каждой группе не более шести простых чисел. Эти числа взаимно просты с 24 по модулю 24.

[ИСН]

мат-ламер в сообщении #1631137 писал(а):

Эти числа взаимно просты с 24 по модулю 24.

Но ведь таких чисел 8.

[мат-ламер]

ИСН в сообщении #1631138 писал(а):

Но ведь таких чисел 8.

Да, правильно. Невнимательно подсчитал. Но для начала получили нужное утверждение в более слабой версии - с заменой четвёрки на тройку. Я думаю, что с помощью компьютера эту константу можно ещё поднять.

-- Вт фев 27, 2024 18:16:31 --

мат-ламер в сообщении #1631140 писал(а):

Я думаю, что с помощью компьютера эту константу можно ещё поднять.

Загуглив "таблица простых чисел", увидел, что до 120 находится всего лишь 30 простых чисел.

[Dmitriy40]

мат-ламер в сообщении #1631140 писал(а):

Загуглив "таблица простых чисел", увидел, что до 120 находится всего лишь 30 простых чисел.

Это мало о чём говорит, ведь в ряду простых встречаются участки сгущений, например 21 простое начиная с 39433867730216371575457664399 укладываются в интервал длиной всего 84 (с +0 по +84), т.е. ровно в 4 раза. Зато сгущений (k-tuples) длиннее 21 простых на четырёхкратных интервалах уже не бывает (за исключением начала числового ряда). Вот это и можно использовать, наверное.

Хотя гораздо проще доказать что в любом интервале длиной $7\#=210$ не более 48 простых (кроме возможно первых, которые проверить вручную и убедиться что везде не более 47), т.е. меньше $7\#/4=210/4=52.5$. Что и доказывает исходную посылку.

-- 27.02.2024, 18:19 --

PS. Для условия $p_n>3n$ достаточно интервала $5\#=30$, для условия $p_n>5n$ достаточно интервала $13\#=30030$, для условия $p_n>6n$ достаточно интервала $23\#$. В принципе для любого конечного коэффициента найдётся свой интервал.

[gris]

а по последовательности $q_n=p_n/n$ есть какая-то теория? Переходы через целые получить можно в рукопашную, а вот насчёт дальнейшего поведения?

[мат-ламер]

gris в сообщении #1631155 писал(а):

а по последовательности $q_n=p_n/n$ есть какая-то теория?

Не совсем понял вопрос. Кое-что есть в Википедии .

-- Вт фев 27, 2024 22:26:20 --

Но там про асимптотику. А в задаче вопрос конкретный:

qwert129 в сообщении #1631103 писал(а):

Найдите наименьшее k, для которого верно неравенство $p_n>4n$

Может вы попробуете на компьютере найти точный ответ?

-- Вт фев 27, 2024 22:32:02 --

Dmitriy40 в сообщении #1631144 писал(а):

Это мало о чём говорит

Но я не претендовал на решение. Это был посыл для ТС, в какую сторону копать.

[gris]

Я имел в виду, что отношение простого к своему номеру всё положе и положе и возникают такие участки
_ n __ p _______________ q ______________
6454 64513 9.995816547877285404400371862
6455 64553 10.00046475600309837335398916
6456 64567 10.00108426270136307311028501
6457 64577 10.00108409478085798358370760
6458 64579 9.999845153298234747599876123
6459 64591 10.00015482272797646694534758
6460 64601 10.00015479876160990712074303
6461 64609 9.999845225197337873394211422
6462 64613 9.998916744042092231507273290
6463 64621 9.998607457836917840012378153
6464 64627 9.997988861386138613861386139
6465 64633 9.997370456303170920340293890
6466 64661 10.00015465511908444169502011
6467 64663 9.998917581567960414411628267
6468 64667 9.997990105132962275819418677
6469 64679 9.998299582624826093677539032
6470 64693 9.998918083462132921174652241
6471 64709 9.999845464379539483851027662
6472 64717 9.999536464771322620519159456
6473 64747 10.00262629383593387919048355

То есть, только простое превысило $10n$, как отношение ушло назад, потом вперёд, назад и окончательно вперёд.
Я к тому, что для $4n$ найти минимум просто и доказать минимальность вполне возможно, а вот для $10n$ переход даже в Энциклопедии есть, но далее идёт шлейф колебаний. Для больших $n$ этот шлейф может растягиваться на миллиарды. И как там искать число, последнее в этом шлейфе, о чём, собственно, и спрашивает ТС.
Тема интересна обобщениями

Ой, да там куча теорий и практик!
Как же приятно впервые в жизни прикоснуться к чуду, хотя бы и давно всем известному.
Лучше через альфу смотреть, но там сложновато.

[мат-ламер]

gris в сообщении #1631165 писал(а):

И как там искать число, последнее в этом шлейфе, о чём, собственно, и спрашивает ТС.

Ну, какую-то оценку наверное можно получить с помощью неравенства Чебышёва (что в той статье в Википедии). Но боюсь, что грубую. И я не понял, начиная с какого числа неравенство Чебышёва справедливо. Точнее, как константы в этом неравенстве зависят от $n$ (считая, что это неравенство не про асимптотику, а является точным, начиная с некоторого числа).

-- Вт фев 27, 2024 23:51:01 --

Хотя для оценки количества $\pi (n) $ простых чисел меньше числа $n$ можно воспользоваться неравенством $\pi (n) < \int\limits_{2}^{n} \frac{ dt }{ \ln{t} }$ , которое будет точным (наверное), начиная с достаточного небольшого $n$ .

И это неравенство для десятки даёт оценку, что в ряде натуральных чисел до $68500$ не более $6850$ простых. И для любого $n$ большего 68500, количество простых чисел меньших его, не превышает $n/10$. Хотя может это и слишком грубая оценка.

[Dmitriy40]

gris в сообщении #1631165 писал(а):

Я к тому, что для $4n$ найти минимум просто и доказать минимальность вполне возможно, а вот для $10n$

Для доказательства $p_n>10n$ достаточно взять интервал $257\#\approx1.65\cdot10^{103}$.
Реально граница будет достигнута сильно раньше, уже при $p_n>e^{10}\approx22000$, в соответствии с формулой $n=\pi(p_n)=p_n/\ln p_n$. Но это в среднем, для нивелирования начального выброса можно взять больше в несколько раз (или поискать более точную доказанную верхнюю границу), а остаток в начале проверить прямо. Во всяком случае это ориентир где искать чтобы не проверять весь вон тот огромный интервал.

-- 27.02.2024, 23:09 --

мат-ламер в сообщении #1631166 писал(а):

неравенством $\pi (n) < \int\limits_{2}^{n} \frac{ dt }{ \ln{t} }$ , которое будет точным (наверное), начиная с достаточного небольшого $n$ .

Не будет.
И кажется есть даже гипотеза/теорема что разность $\pi(x)-\operatorname{Li}(x)$ меняет знак бесконечное число раз.

[Dendr]

мат-ламер в сообщении #1631140 писал(а):

Загуглив "таблица простых чисел", увидел, что до 120 находится всего лишь 30 простых чисел.

При этом замечаем, что $\varphi(120)=32$. То есть среди чисел от 121 до 240 ровно 32 числа взаимно просты с 120, то есть среди них не более 32 простых, откуда следует (без проверки по таблице), что есть не более 62 простых чисел, меньших 240.

И если удастся как-то формально показать, что среди этих 32 "кандидатов" попадется хотя бы два составных числа. Но это действительно так (!). Составим из них наборы с одинаковым остатком от деления на 7:
$0: 7, 49, 77, 91, 119$
$1: 1, 29, 43, 71, 113$
$2: 23, 37, 79, 107$
$3: 17, 31, 59, 73, 101$
$4: 11, 53, 67, 109$
$5: 19, 47, 61, 89, 103$
$6: 13, 41, 83, 97$
Таким образом, среди чисел $\left{120m+1, ..., 120(m+1)\right}$ по крайней мере 4 будут делиться на 7. Следовательно, среди каждых 120 чисел (кроме первых) встретится самое большее 28 простых чисел.

Это дает нам очень грубую (но пригодную для решения данной задачи) оценку $\pi(120m)\le28m+2$. Теперь мы можем "ручками" перебрать простые числа до 240 и убедиться, что ответ на задачу $k=31$. Так же выясняем, что "плюс два" можно выкинуть уже для $m=2$, что дает возможность полагать $p_{28m+1}>120m>112m+4$ и это создает зазор (размера $8m-4$), который позволит "впустить" большое количество близнецов - их может быть, как видно, не более 14 пар, что сократит отставание не более чем на 28, то есть $8m-4\ge28 \Leftrightarrow m\ge4$ позволяет гарантировать, что промежуточные простые числа не спустятся ниже $4n$. 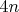Опять же, "ручная" проверка показывает, что до 480 этого не случается - а дальше автоматически удастся.

Для бОльших множителей, видимо, можно поиграться с факториалами (праймориалами) больших чисел и выяснить, какие у них значения функции Эйлера - чем меньше, тем лучше, и среди них фиксируем остатки от деления на наименьшее простое из них. Найти наименьшее $k$ может, и не удастся, но доказать, что оно существует, возможно.

P.S. Вообще, пики $\frac{n}{\varphi(n)}$ много чего дадут

[vicvolf]

qwert129 в сообщении #1631103 писал(а):

Пусть $p_n$ это $n$-ное простое число. Найдите наименьшее k, для которого верно неравенство $p_n>4n$ для всех натуральных $n\ge k$ и докажите это неравенство. (Я хотел доказать по индукции, но ничего не получилось, хотелось бы увидеть элементарное доказательство без теоремы о простых числах)

Прахар "Распределение простых чисел" стр. 27 Теорема 3.3 Пусть $p_n$ есть $n$-ое простое число $n \geq 8$. Тогда $p_n >cn\ln(n)$, где $c$ - постоянная. Отсюда следует, что с некоторого значения $k$ для $n \geq k$ выполняется $p_n>4n$ и вообще $p_n>Cn$, где $C$ - любая положительная постоянная. Для $p_n>4n$ значение $k=31$ ($p_{31}=127, 4k=124$).