Какое у Вас определение инвариантности?
Общепринятое в наше время понимание. Не из старинных статей Лоренца и Пуанкаре с их вербальной невнятицей, а из учебников по теории поля, написанных уже после создания СТО. Из начальных глав учебников, где идёт речь о преобразованиях Лоренца (
ПЛ) и вводится мат. аппарат с 4-векторными и тензорными обозначениями. В ЛЛ-2 это §1-§7. В упомянутой Вами книге Паули "Теория относительности" см. гл. II; в §9 виден один из примеров инвариантной величины - важное для нас выражение

где

и

это 4-векторы:

.
Если вкратце, то слово "инвариантность" означает "неизменность". А чего именно неизменность - это сильно зависит от контекста, и в деталях раскрывается только на языке математики. Есть просто неизменность числового значения функции при замене её аргументов по формулам ПЛ. А бывает и неизменность самой формы функции, в которой в неё входят её аргументы. Инвариантность системы дифф. уравнений - это неизменность формы уравнений, в которой в них входят функции; при этом форма самих функций в общем случае изменяется при ПЛ. (Всё нужное более или менее у нас здесь уже было: об инвариантах, о 4-векторах и, в частности, о 4-скорости я напоминал
в этом сообщении.)
Вопрос, который Вы проигнорировали: у Вас сколько времен в формулах? У Шотта это одно время - текущее время (момент измерения полей). У ЛЛ-2 это также одно время, t' должно быть выражено через x,y,z,t.
И у меня одна независимая переменная

У меня формулы потенциалов ЛВ те же, что в ЛЛ-2; только вместо

я пишу

чтобы избежать путаницы, потому что мы везде в этой теме штрих используем для обозначения величин, наблюдаемых из другой ИСО. Да,

не есть вторая независимая переменная времени, а определяется (неявно, сложным уравнением) как функция от

Это тоже было:
см. здесь.
если одно, то хотелось бы увидеть, как в формуле для скорости выполняются преобразования и сохраняется вид "инвариантов".
Пусть движение точечного заряда-источника, задано в исходной ИСО некими функциями

сколь угодно сложными. Здесь метка

это ещё не признак конкретной точки на траектории, а просто метка для координат на всей траектории (вместо этого можно было бы написать, например,

но я не стал плодить новых букв для координат).
Уравнение для

есть

где

- 4-координаты точки P, в которой интересуемся потенциалами

; это независимые переменные, аргументы функций

Других независимых 4-координат нет. Если обозначить здесь квадратный корень как

то уравнение для

запишется кратко в виде

В общем случае функцию

в явном виде не найти, да. Однако ясно, что для каждой точки Р существует своё конкретное значение

Поэтому существуют и значения

свои для каждой точки Р; дальше я обозначаю такие числа для краткости просто как

Для каждой точки P соответствующие ей четыре числа

определяют конкретную точку Q (свою для каждой точки Р) на мировой линии частицы-заряда, а уравнение для

связывает разности 4-координат мировых точек P и Q:

Такая связь означает, что отрезок прямой в пространстве-времени, проведённый из Q в P, т.е. "4-вектор" с компонентами

светоподобен. Действительно, возведя обе стороны в квадрат, получаем равенство

то есть

Как всё опишется в другой ИСО? По принципу относительности все ИСО равноправны. Поэтому, такое же рассмотрение в другой ИСО', со штрихованными 4-координатами, заведомо даст нам такие же формулы, только все величины в них будут с самого начала штрихованные. И поскольку переход от одной ИСО к другой обязан описываться в СТО лоренц-преобразованием, то связаны штрихованные величины с нештрихованными окажутся формулами ПЛ. Как говорится, им от этого никуда не деться.
В этом легко убедиться прямо. Для описания траектории того же самого заряда в другой ИСО, в формулы ПЛ надо подставить в качестве

функции



Получилось параметрическое описание мировой линии в штрихованной ИСО, параметром служит переменная

Штрихованные 4-координаты точки Q на мировой линии это их значения при определённом значении параметра:

им соответствуют нештрихованные значения 4-координат

в исходной ИСО. Обозначим эти штрихованные значения по аналогии с нештрихованными - без значения аргумента, т.е.:




Тогда:


Для 4-координат

точки P формулы ПЛ будут такие же, только без метки Q (для краткости не выписываю их). Значит, составив разности 4-координат точек P и Q, получим для разностей снова формулы ПЛ:


Поскольку, как видим, величины

преобразовались по формулам ПЛ для 4-координат, эти величины являются компонентами 4-вектора именно в точном смысле термина "4-вектор". И, значит, комбинация

инвариантна - её форма и значения не изменяются при ПЛ 4-координат точек P и Q:

Для светоподобного 4-вектора эта величина равна нулю. Так что, если в исходной ИСО

то и в другой ИСО'

Ничего иного и не следовало ожидать. Ведь это математические азы СТО: 4-координаты
любых мировых точек, а с ними и разности 4-координат
любых мировых точек преобразуются по формулам ПЛ, - как компоненты

вообще любого 4-вектора. Скалярное произведение

любых двух 4-векторов (в том числе и в случае, когда это один и тот же вектор), есть величина инвариантная (по форме и по значению) к ПЛ:


// Сложных формул у нас нет, поэтому не различаю верхние и нижние индексы; просто помним, что в суммы по повторяющимся индексам временные и пространственные компоненты входят с противоположными знаками. Равенство

легко проверяется, не выписываю доказательство. // Всё это верно для
любых точек в пространстве-времени, и для
любым образом соединяющих их отрезков прямых - они являются 4-векторами, т.е. их проекции на 4-координатные оси преобразуются по обычным формулам ПЛ для 4-координат.
В частности, все эти азы СТО верны для любых точек Q на мировой линии заряда, и для любых точек P вне мировой линии заряда. Пусть мировая линия задаётся супер-ультра-зашибись сложными функциями

так что уравнение

для точек Q, соответствующих произвольным точкам P, в явном виде не решит и сам чёрт. Невозможность в явном виде найти решение не отменяет факта, что разности 4-координат точек Р и Q преобразуются как компоненты

4-вектора, и что скалярное произведение этого 4-вектора с любым 4-вектором (с каким-угодно 4-вектором
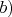
будет инвариантной величиной - не изменяющейся при ПЛ:

4-скорость

в точке Q мировой линии можно представлять себе как очень маленький и поэтому практически прямолинейный отрезочек

мировой линии (отрезочек с началом в точке Q и концом в близкой "будущей" точке мировой линии) с инвариантным множителем

Это определение становится точным при устремлении концевой точки отрезочка к точке Q.
Поскольку разности 4-координат двух точек заведомо преобразуются как компоненты 4-вектора, то из указанного описания 4-скорости

явствует, что 4-скорость есть 4-вектор; его скалярное произведение на самого себя - инвариант, равный единице:

Как и скалярное произведение любых 4-векторов в СТО, скалярное произведение 4-скорости в любой точке мировой линии вообще с любым 4-вектором заведомо является инвариантной величиной - не изменяющейся при ПЛ. Как частный случай и скалярное произведение 4-скорости в точке Q со светоподобным 4-вектором QP есть инвариант:

Повторю: этот факт не отменяется отсутствием в общем случае
явных формул для 4-координат точек Q. Явные формулы оказались не нужны для доказательства в общем виде инвариантности величины

Без явных формул нет возможности в них что-либо подставлять явно; только и всего. (Притом, в принципе, всегда есть возможность численно задавать густую сетку точек P и решать уравнение для координат точек Q численными методами.)
Более подробное объяснение методу дано у Паули, Теория относительности, §32. Но Паули ни слова не говорит, что

(ф-ла 238а) есть инвариант.
Не говорит по той же причине, по какой он не повторяет на каждом шагу "2х2=4". Всю нужную информацию о законах преобразования встречающихся в теории величин Паули дал в главе II "Математический аппарат"; вот там он и сказал про инвариантность комбинаций вида

см. уже упомянутый
скриншот.
Если скорость заряда

имеет две компоненты (например, заряд вращается), что по Вашему мнению означает инвариантность

Тем более после преобразований Лоренца новые координаты и время не будут на световом конусе.
(В цитате я заменил латинский индекс

греческим

. У нас, как и в ЛЛ-2, латинские индексы пробегают 4 значения, поэтому пусть три значения

пробегают греческие индексы.) Насчёт "не будут на световом конусе" - грубая ошибка. Опять-таки азы СТО: светоподобный интервал светоподобен во всех ИСО. Раз уж

в исходной ИСО, то и в любой другой ИСО'

Ну а как конкретно движется заряд, это для инвариантности величины

совершенно неважно. Пусть заряд хоть вращается, хоть какие угодно кренделя вытанцовывает. В любом случае в исходной ИСО в каждой точке его траектории

у заряда есть своя для данной точки 3-скорость

Как уже говорилось, для заданной точки наблюдения

существует решение

- прошлый момент времени, - которым определяется соответствующая этой точке P точка Q на траектории заряда; 4-координаты этой точки Q обозначаем как

Скорость заряда в этой точке Q обозначаем как

Её величиной определяется для точки Q число, которое мы называем "гамма на траектории заряда в точке Q", это

Компоненты 4-скорости в точке Q даются упоминавшимся выше определением

где компоненты 4-вектора

это

Можно представлять их себе как приращения к 4-координатам точки Q. С учётом равенства

имеем для компонент 4-скорости в точке Q выражения:

Поэтому скалярное произведение 4-скорости с 4-вектором QP, имеющим компоненты

и

есть:

Инвариантность величины

означает вот что. В другой ИСО' у той же пары точек P и Q мировые координаты примут другие значения (штрихованные), и форма мировой линии заряда будет выглядеть как-то иначе, так что 3-скорость заряда и гамма на траектории заряда в точке Q будут иные (штрихованные), но само выражение через штрихованные величины и значение

останется неизменным:

Но допускаем, что в форме

- существуют два времени t, t'.
В такой формуле я вместо

пишу

так как штрих у нас занят для другой ИСО. Говорить, что времён тут два, я бы стал только с важным пояснением: время

не есть независимая переменная, а является функцией (в явном виде нам неизвестной в общем случае) от независимых переменных - от 4-координат

точки наблюдения P полей. Соответственно, и у полей независимой переменной времени является одно время

а не две независимых переменных

Давайте, возьмем выражения Шотта

Теперь преобразовываем координаты по формулам

. Получаем

<...> Какая из этих форм инвариантна? И как одну из форм свести к

?
Вторая форма, о которой говорится в цитате, это

Вместо вашего обозначения

я буду писать

(буква

занята для векторного потенциала). Выражения для инвариантов (при ПЛ вдоль x-оси)

и
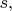
зависящих от

и декартовых координат

точки Р наблюдения поля, я выписал в
предыдущем сообщении.
Видно, что форма

не инвариантна: её зависимость от новых переменных

не такая, как от

Вторую форму рассмотрим подробнее. Выпишу все полезные выражения (хотя ниже все они мне не потребуются), которые получаются в исходной ИСО в ходе решения уравнения

для задачи с траекторией заряда

(гиперболическое или, что то же, равноускоренное движение):




Видно, что так как

то получается:

Это, как мы уже знаем, инвариантная (к ПЛ вдоль x-оси) комбинация переменных

являющихся 4-координатами произвольной точки P наблюдения поля.
(Результат

можно получить и другим, более длинным, но притом, может быть, более наглядным путём: полагаясь на заведомую инвариантность формы

можно перейти в специальную ИСО (свою для каждой точки P), такую, в которой

и, следовательно,

В такой ИСО'


и прямое вычисление расстояния

с учётом в выражении для

уравнения

даёт:

Наглядность здесь в том, что инвариант

получает интерпретацию в терминах расстояния

между точками P и Q в специальной ИСО'. Притом легко для точек P c равными нулю

и

проиллюстрировать всё рисунками в двух ИСО с гиперболической мировой линией (по аналогии с приводившимися мной рис.1 и рис.2 для другой мировой линии заряда); рекомендую в качестве упражнения.)